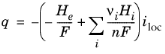where q is the boundary heat source (W/m
2),
n and
νi are the number of electrons participating in the reaction and the stoichiometric coefficients of the reaction, respectively, and
iloc local current density at the electrode surface. Subscript
e above denotes the electron, and
i the electrolyte phase species.
where ΔH is the potential-independent net partial molar enthalpy change, defined as
where ΔG is the Gibbs free energy of the reaction, and where
ΔS is the net entropy change, and defining the equilibrium potential as
The total heat source due to the electrochemical reactions, qEC, for an electrode surface is the sum of all individual heat sources of the electrode reactions according to
where m is the index of the electrode reaction.