Use the Eigenvalue Solver (

) to find the solution to linear or linearized eigenvalue problems (also called eigenfrequency problems). This solver is automatically used when an
Eigenvalue or
Eigenfrequency study is added to the model.
Also see The Eigenvalue Solver Algorithms. The solver settings are split in the following sections
Use the Defined by study step list to specify if the settings are synchronized with the corresponding study step. Select
User defined to specify the properties below (in addition to the relative tolerance and the options for computing and storing left eigenvalues, which are always available).
The settings here are similar to those for the Eigenvalue study step, with the following exceptions and options, when applicable:
From the Eigenvalue transformation list, select a transformation method for transforming the eigenvalues into another related quantity. The default is
None, which keeps the original eigenvalues. Depending on the physics in the model, other transformations might also be available.
The number in the Relative tolerance field (default 1.0·10
−6) controls the relative error in the computed eigenvalues.
From the Compute and store left eigenvectors list, choose
Automatic (the default),
On, or
Off. The
Automatic option typically is the same as
Off, but, depending on the other settings, if needed, the left eigenvectors will be computed (and eventually stored). The eigenvectors referred to as just “eigenvectors” are right eigenvectors. A left eigenvector is defined as a row vector
XL that satisfy
XL A = λLXL . For example, for sensitivity and optimization, when the matrices are nonsymmetric, left eigenvectors will be computed. Also, left eigenvectors can be used for projecting equations in the modal solver.
Select the Enter transformed values checkbox to enter the values to search around as the transformed value (an eigenfrequency, for example) instead of the corresponding eigenvalue.
Under FEAST settings, the default setting for the
Integration type for estimation list and the
Number of integration points for estimation list is
Automatic. When you choose
Automatic in the
Integration type for estimation list, it uses the Gauss type for real symmetric or Hermitian eigenvalue solvers and the trapezoidal method for other types of solver. Otherwise, choose
Gauss or
Trapezoidal to use only one of those methods. When you choose
Automatic in
Number of integration points for estimation, it is 6 for real symmetric or Hermitian eigenvalue solvers and 16 for other types of solvers.
Select the Distribute linear system solution checkbox to run the FEAST eigenvalue solver in parallel. See
Running FEAST in a Parallel MPI Mode for more information.
When you have selected the A posteriori residual check checkbox, the solver a posteriori explicitly computes the relative residual of the eigenpair and checks that this quantity is smaller that 100*
tol, where
tol is the
Relative tolerance. Notice that, in order to do this computation, the solver needs to store the
K,
D, and
E matrices, and therefore, this option requires more memory. If any residual is larger than the tolerance, a
Warning node appears with information about which eigenpairs it concerns. That information also appears in the solver log.
If the eigenvalue itself appears nonlinearly, and the solver is not the ARPACK nonlinear solver, the solver reduces the problem to a quadratic approximation around an eigenvalue linearization point. Under Eigenvalue linearization point, select the
Transform eigenvalue linearization point checkbox to transform the linearization point value using the selected eigenvalue transformation. Specify the value of the linearization point in the
Value of eigenvalue linearization point field (SI unit: rad/s).
If you use the ARPACK nonlinear solver, the solver approximates the nonlinearity in the eigenvalue with a polynomial and, if you have selected the Quasi-Newton refinement checkbox, it will activate extra quasi-Newton iterations on the returned solutions given by the ARPACK call. The
Maximum number of iterations (default: 20) does what the name suggests. The
Tolerance factor (default: 1) instead makes it possible to refine the solutions more accurately. More precisely, the tolerance for stopping the quasi-Newton refinement process is the product between the values for the
Tolerance factor and the
Relative tolerance.
For other settings, see the Eigenvalue or
Eigenfrequency study settings. When the eigenvalue search settings are defined by the study step, the settings above that correspond to similar study settings are not available.
This section is only visible when the study contains a Stationary Then Eigenfrequency study step. It can be used to specify which dependent variables are computed with the Eigenvalue solver. The same dependent variable cannot appear in the equivalent section of the
Stationary Solver, control variables excepted.
From the Linearity list, choose
Linear (the default) or
Linear perturbation.
|
•
|
Initial expression (the default) to use the expressions specified on the Initial Values nodes under a specific physics interface as a linearization point.
|
|
•
|
Solution to use a solution as linearization point.
|
Use the Solution list to specify which solution to use if
Prescribed by is set to
Solution:
|
•
|
Select Zero (the default) to use a linearization point that is identically equal to zero.
|
Select the Store linearization point and deviation in output checkbox to store the linearization point and the deviation from that linearization instead of the total solution.
Select an option from the Scaling of eigenvectors list to specify the scaling method used to normalize the eigenvectors. Select:
|
•
|
RMS to use root mean square normalization. This RMS scaling of the eigenvector u is such that  .
|
|
•
|
Maximum to use maximum norm normalization. The degree of freedom with the largest absolute value will be assigned the value specified in the Maximum absolute value field (default: 1), so that 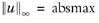 . You can change the maximum absolute value to, for example, keep the eigenmodes small in value. The physics interfaces for structural mechanics set this value to a small number during the solver generation.
|
|
•
|
Mass matrix to scale the eigenvectors such that the modal masses become unity.
|
Select User defined from the
Defined by study step list in the
General section to specify the settings below for sorting and filtering the eigenmodes. Those settings can be useful to, for example, filter out physically uninteresting solutions or to sort the solutions according to given criteria.
The eigenvalues can be excluded if there is a filter expression that they do not satisfy. In the table below, in the Filter expression (store if true or >0) column, add expressions for the filtering Those expressions can be functions of the eigenvalue
lambda or eigenfrequency
freq and can be logical expressions such as
lambda>10. If desired, add some descriptive text in the
Description column for the expressions.
The Store solutions list is always available: Choose
All converged solutions (the default) or
First Nth for the first
Nth solutions. Then specify that number in the
Maximum number of stored solutions field (default: 1000).
The eigenvalues can be sorted in Ascending (the default) or
Descending order depending on the
Ordering setting. When the
Sorting method is
Predefined, you can choose to
Sort primarily based on the
Real part,
Imaginary part,
Real part magnitude,
Imaginary part magnitude, or
Absolute value. The same settings are available for the
Sort secondly option, which is used to resolve conflicts. The defaults for eigenvalues are
Real part for
Sort primarily and
Imaginary part magnitude for
Sort secondly. For eigenfrequencies, the defaults are
Imaginary part for
Sort primarily and
Imaginary part magnitude for
Sort secondly. Also, the
Sort based on transformed eigenvalues checkbox is selected by default to take and eigenvalue transformation into account when sorting.
Alternatively, Manual can be chosen for the
Sorting method and then an arbitrary number of (ordered) custom sorting priority expressions can be defined in the table that appears. In the
Sorting priority expression column, add expressions for the sorting, in order of priority. Those expressions can be functions of the eigenvalue
lambda or eigenfrequency
freq. For example, you can specify an expression such as
abs(freq-1) to sort according to the distance from a given shift (1 in this case). If desired, add some descriptive text in the
Description column for the expressions.
The Conjugate-pair consecutive sort checkbox is selected by default to make sure that complex-conjugate eigenpairs appear one after the other, regardless of the sorting rules.
The eigenvalue solver is an iterative algorithm. Use the Maximum number of eigenvalue iterations field to limit the number of iterations (default: 300).
When you use the ARPACK solver, you can use the Dimension of Krylov space field to control the algorithm’s memory use. The default value of 0 means that the solver sets the dimension automatically to approximately twice the number specified in the
Desired number of eigenvalues field in the
General section.
Click the Add button (

) to add a constant and then define its name in the
Constant name column and its value (a numerical value or parameter expression) in the
Constant value column. By default, any defined parameters are first added as the constant names, but you can change the names to define other constants. Click
Delete (

) to remove the selected constant from the list.
The Log section contains logs of the eigenvalue solver results and properties of the assembled system, including the solver iterations and the total solution time. This log is stored in the Model MPH-file.
|
|
Conical Quantum Dot: Application Library path COMSOL_Multiphysics/Equation_Based/conical_quantum_dot
|