The Modified Reynolds Equation — Gas Flow
Thin-film gas flow is often isothermal, and in many cases the ideal gas law can be assumed. The ideal gas assumption relates the gas density to the pressure as
here, T0 is the (constant) temperature of the gas, Mn is the molar mass, and R is the universal gas constant. The total gas pressure, pA = pref + pfilm, is written in terms of the reference pressure level pref and the pressure developed in the thin-film flow, pfilm. Substituting this density into Equation 9-3 and dividing it by Mn/RT0 results in the modified Reynolds equation for ideal (isothermal) gases:
(9-13)
The average flow rate and the forces acting on the walls are computed in the same manner as for the standard Reynolds equation.
When the Compute implicit height change from wall velocity checkbox and/or Compute implicit height change from base velocity checkbox are selected, the height changes due to the wall and/or base velocity are computed as,
(9-14)
The wall and base velocities effectively induce mass sources and which are added to the right-hand side of Equation 9-13, with,
(9-15)
Slip Boundary Condition for Gases
For a gas, the slip length is often expressed using the mean free path, λ, and a tangential momentum accommodation coefficient, α. The following definition of the mean free path is used in the Thin-Film Flow interfaces:
where μ is the gas viscosity, p is the gas pressure, R is the molar gas constant, T is the temperature, and Mn is the molar mass of the gas. This definition differs from the equivalent free path in Ref. 3 by a factor .
The slip length is then defined as
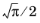
Values for the a tangential momentum accommodation coefficient, α for various gas- surface combinations are given in Ref. 2.