The SSG-LRR model belongs to RANS-RSM type of turbulence models and, hence, does not assume a particular form of 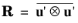(the kinematic Reynolds stress tensor). It solves the transport equation for R instead, complemented by the transport equation for the turbulence specific dissipation rate ω, which allows to capture the evolution of turbulence structure properly Ref. 33. This leads to more accurate prediction of separation, transient phenomena, effects of swirl and curvature. Moreover, correct description of secondary flows is achieved, which eddy-viscosity based models are intrinsically incapable of.

The set of SSG-LRR model parameters with their default values is

Similar to The SST Turbulence Model the model parameters are blended between ω-based and ε-based approaches as

The interpolation function F1 is defined as

where lw is the distance to the closest wall.

The R-equation is stated as

This is a symmetric tensor equation that consists of six scalar equations. The production term Pij (as well as P - production term of k) has explicit form,

Of primary importance for a Reynolds Stress Model is the modeling of the pressure–strain correlation Πij:

which is responsible for the redistribution of the turbulence kinetic energy among the components of R. For SSG-LRR it involves seven model parameters (after the blending is performed).

The turbulent diffusion D is modeled as a “simple diffusion”and turbulent dissipation εij of R is modeled as isotropic

The ω-equation is stated as

The wall distance variable, lw, is provided by a mathematical Wall Distance interface that is included when using the SSG-LRR model. The solution to the wall distance equation is controlled using the parameter lref. The distance to objects larger than lref is represented accurately, while objects smaller than lref are effectively diminished by appearing to be farther away than they actually are. This is a desirable feature in turbulence modeling since small objects would get too large an impact on the solution if the wall distance were measured exactly.

When there is no Moving Mesh, the equation for the wall distance variable can be solved once only. A Wall Distance Initialization study type is provided for this purpose and should be added before the actual Stationary or Time Dependent study step.

The SSG-LRR turbulence model can be integrated all the way down to the wall and is consistent with the no-slip condition u = 0. Since fluctuations of velocity must disappear on the wall, so must R. Hence, R = 0 on the wall.

The corresponding boundary condition for ω is

To avoid the singularity at the wall, ω is not solved for in the cells adjacent to a solid wall. Instead, its value is prescribed by Equation 3-195 (using the variable ωw, which only exists in those cells). Accurate solutions in the near-wall region require that the wall resolution in viscous units

where the resolution height is based on the distance between the first computational node inside the domain and the wall. uτ is the friction velocity which is calculated from the wall shear-stress τw,

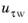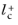
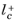
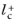
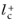
and is available as the postprocessing variable (u_tauWall). Also, the boundary variable Distance to cell center in viscous units, (lplus_cc), is available to ensure that the mesh is fine enough. is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell, thus and according to Equation 3-196 should be about 0.5. Observe that very small values of can reduce the convergence rate. Also notice that it is unlikely that a solution is obtained at all if

Since the ωw variable requires the wall distance, a wall distance equation must be solved prior to solving the SSG-LRR model.

The postprocessing variable Wall resolution in viscous units, (Delta_wPlus), is available.

The guidelines given in Inlet Values for the Turbulence Length Scale and Turbulent Intensity for selecting the turbulence length scale, LT, and the turbulence intensity, IT, apply also to the SSG-LRR model.

The SSG-LRR model essentially has the same default initial guess as the SST model, but for the Reynolds stress tensor instead of k:

The default initial value for the wall distance equation (which solves for the reciprocal wall distance) is 2/lref.

The Wilcox R-ω model applies absolute scales of the same type as the SST model, namely