The k-
ω model solves for the turbulent kinetic energy,
k, and for the dissipation per unit turbulent kinetic energy,
ω.
ω is also commonly know as the specific dissipation rate. The CFD Module has the Wilcox revised
k-
ω model (
Ref. 1)
(3-107)
(3-108)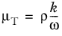
(3-109)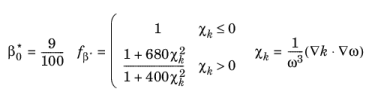
where in turn Ωij is the mean rotation-rate tensor
and Sij is the mean strain-rate tensor
Pk is given by
Equation 3-91. The following auxiliary relations for the dissipation,
ε, and the turbulent mixing length,
l∗, are also used:
(3-110)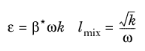
The implementation of the k-
ω model relies on the same concepts as the
k-
ε model (
Ref. 10). This means that the following approximations have been used:
where lr is the limit given by the realizability constraints (
Equation 3-96 and
Equation 3-97).
(3-111)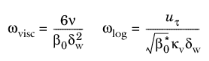
(3-112)
where δw is the distance to the nearest wall,
κv, is the von Kármán constant (default value 0.41),
U|| is the velocity parallel to the wall, and
B is a constant that by default is set to 5.2. Menter and others (
Ref. 9) suggested the following smooth blending expressions for
ω and
uτ:
(3-113)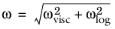
(3-114)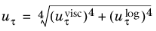
These expressions can be combined with the lift-off concept shown in Figure 3-7 which gives
δw = hw/2. The wall condition for
ω is given by
Equation 3-113 and the conditions for the momentum equations are a no-penetration condition
u ⋅ n = 0 and a shear stress condition
(3-115)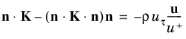
The k-equation formally fulfills
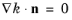
both at the wall and in the log-layer, so this condition is applied for all
δw+.
The system given by Equation 3-98 through
Equation 3-115 are, however, nonlinear in
uτ and not very stable. To circumvent this, a variable
u∗,log is introduced (see
Ref. 10 and
Ref. 11) such that
(3-116)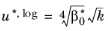
(3-117)
Equation 3-117 is in turn is used to calculate an alternative dimensionless wall distance
(3-118)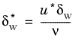
Equation 3-117 is used instead of
uτ in the expression for
ωlog and
Equation 3-118 is used instead of
δw+ in the expression for
uτlog. The traction condition in
Equation 3-115 is replaced by
(3-119)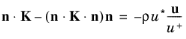
The postprocessing variable for friction velocity uτw (
u_tauWall) is based on the effective traction at the wall and is defined as
When Wall Treatment is set to Wall functions, wall boundaries are treated with the same type of boundary conditions as for the
k-
ε model (see
Wall Functions) with
Cμ replaced by
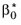
and the boundary condition for
ω given by
(3-120)
The k-
ω turbulence model can be integrated all the way down to the wall and is consistent with the no-slip condition
u = 0. Since all velocities must disappear on the wall, so must
k. Hence,
k = 0 on the wall.
(3-121)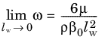
To avoid the singularity at the wall, ω is not solved for in the cells adjacent to a solid wall. Instead, its value is prescribed by
Equation 3-121 (using the variable
ωw, which only exists in those cells). Accurate solutions in the near-wall region require that the wall resolution in viscous units
(3-122)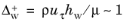
(3-123)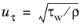
and is available as the postprocessing variable 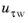 (u_tauWall
(u_tauWall). Also, the boundary variable
Distance to cell center in viscous units,
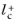
(
lplus_cc), is available to ensure that the mesh is fine enough.
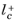
is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell, thus
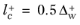
and according to
Equation 3-122 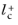
should be about
0.5. Observe that very small values of
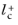
can reduce the convergence rate.
Since the ωw requires the wall distance, a wall distance equation must be solved prior to solving a
k-
ω model with low-Reynolds-number wall treatment.
The postprocessing variable Wall resolution in viscous units,
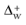
(
Delta_wPlus), is available.
The k-
ω model applies absolute scales of the same type as the
k-
ε model (see
Scaling for Time-Dependent Simulations) except that the scale for
ω is given by
The k-
ω model can in many cases give results that are superior to those obtained with the
k-
ε model (
Ref. 1). It behaves, for example, much better for flat plate flows with adverse or favorable pressure gradients. However, there are two main drawbacks. The first is that the
k-
ω model can display a relatively strong sensitivity to free stream inlet values of
ω. The other is that the
k-
ω model is numerically less robust than the
k-
ε model.
