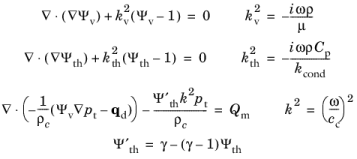The SLNS formulation is based on a Helmholtz decomposition of the full set of governing equations of the The Thermoviscous Acoustics, Frequency Domain Interface as derived in the Acoustic Perturbation and Linearization section. The resulting three scalar Helmholtz equations are solved sequentially. These are for the viscous scaling function Ψv, the thermal scaling function Ψth, and the acoustic pressure p. The main assumption for the decomposition is that the acoustical wavelength is much larger than the thickness of the viscous and the thermal boundary layers. See also Ref. 11 and Ref. 12.

The three equations solved are for the viscous scaling function Ψv, the thermal scaling function Ψth, and the total acoustic pressure pt. The equations are

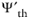
where kv is the viscous wave number, kth is the thermal wave number, and k is the wave number of the compressional acoustic wave. is the modified thermal scaling function. The condition, for the validity of the Helmholtz decomposition, reads

where δv is the viscous boundary layer thickness and δth is the thermal boundary layer thickness. This means that the wavelength of the compressible pressure wave has to be much larger than the thermal and viscous boundary layers.