The Electrostatics Interface has an option to use The D-V Formulation. This is accessed through the discretization options in the electrostatic interface settings. This formulation is available for 2D and 3D components. The difference with this formulation compared to the default V formulation used in Electrostatics is that instead of solving only for the Electric potential, V, the D-V formulation is a mixed formulation method that simultaneously solves for two dependent variables. These are the flux term, the electric displacement field D, as well as the scalar potential, V.

Computing the flux directly is advantageous for applications where the accuracy of the electric displacement field is important. This is useful for situations that involve large fields in tight geometries, such as comb drives in MEMS devices. Electromagnetic forces are also derived from the flux term, which makes accurate fluxes important in electromechanical applications.

The standard Electrostatics formulation is based on the equations

Having the scalar Electric potential V as the dependent variable reduces the system to one equation to be solved. This is computationally straightforward. However, as the electric field, and in turn the electric displacement field, are derived by differentiating this scalar potential, these terms will be expressed as a lower order polynomial and so have less accuracy.

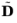
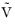
The D-V formulation is a mixed formulation that solves two equations and is developed in a way to set D as a dependent variable along with V. This is achieved using the weak form (see COMSOL documentation on weak form), defining the test functions and , and integrating the above equations over a domain Ω to get

with n being the normal vector on the boundary δΩ.

Here, one equation is posed as a saddle point problem while the other equation acts as a constraint on the first by establishing V as a Lagrange multiplier. This is implemented by using divergence elements for the D-field and a discontinuous scalar Lagrange element for V. In this implementation, V is a lower polynomial order than the D-field. The extra degrees of freedom on the displacement field provide greater accuracy for this flux term. But as a result, the electric potential has a coarser representation though it is still accurate in the integral sense.

The Force Calculation feature and the Electromechanics Multiphysics coupling interface both use the Maxwell Stress Tensor, see Computing Electromagnetic Forces and Torques. When using the D-V formulation, this tensor is computed using the flux terms, D and E with this higher polynomial order.

A consequence of formulating the interface with the flux D-field as the dependent variable is that the types of boundary conditions are swapped. An essential boundary condition in the standard V-formulation is a natural boundary condition in the D-V Formulation and a natural boundary condition becomes an essential one. The features of the Electrostatics interface have been reformulated accordingly.