When solving for the scattered field in 2D axisymmetry, the background wave type can be set to a linearly polarized plane wave propagating in arbitrary direction in the Settings of The Electromagnetic Waves, Frequency Domain Interface. The linearly polarized plane wave is of the form Eb = E0ej(ωt − (k ⋅ r)). In Cartesian coordinates, E0 = (Ex, Ey, Ez), k = (kx, ky, kz), and r = (x, y, z). To express a linearly polarized plane wave with arbitrary incident angle and polarization angle in cylindrical coordinates for a 2D axisymmetric simulation, use the following expansions:

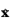
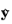
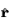
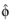
where θ is the angle with respect to the positive z-axis, ϕ is the azimuthal angle, m is the azimuthal mode number, and Jm is the Bessel function of the first kind of order m. Furthermore, the basis vectors and in Cartesian coordinates can be expressed with basis vectors and as

Consequently, a plane wave background field with amplitude E0, incident angle θ, and polarization angle α can be written as (Er, Eϕ, Ez), where

Here, θ and α are defined as the schematic shown in Figure 3-2. Once the linearly polarized plane wave is used as the background field, an auxiliary sweep over the azimuthal mode number will be added. After the simulation, the total scattered field is given by the sum of all the azimuthal modes. The z-components of the scattered field and the background field will be plotted by default. Other components of the field can be computed in a similar way with the help of the sum and withsol operators.
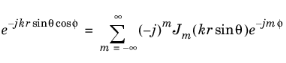