Continuity Condition
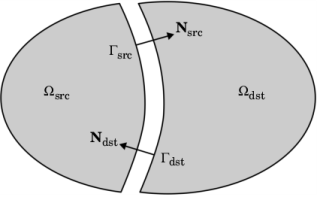
The Continuity node is a way to connect disconnected parts of an assembly by adding constraints or equations on a shared boundary. Consider a problem with two domains Ωsrc and Ωdst with a fully or partially shared boundary Γint such that Γint = Γsrc ∩ Γdst, as is schematically shown in Figure 3-38.
Figure 3-38: Schematic illustration of a continuity interface between two disconnected parts of an assembly.
To enforce continuity between the two domains, the following conditions has to hold on the shared boundary
(3-189)
(3-190)
where Pi is the first Piola–Kirchhoff stress tensor, Ti is the nominal traction, and Ni is the normal vector in the material frame for the respective sides of the interface. The first condition represents the continuity of displacements and the second follows from the Newton’s third law. If the Classical constraints method in the Continuity node is used, pointwise constraints are set up on Γdst to enforce the continuity of displacements given by Equation 3-189. This is accomplished with the help of the mapping operator map(E, x) that is set up by the Identity pair, where E is some generic quantity to be mapped and x is the point to which E is mapped. Using this operator, the constraint equation is written as
where it is here implied that the mapping is made using material coordinates X, and that the mapping is made from Γsrc to Γdst. The above pointwise constraint implicitly enforces the condition given by Equation 3-190. The above constraint equation can also be implemented as weak constraints by introducing Lagrange multipliers.
Another alternative is to use the Nitsche method, which was originally suggested by J. Nitsche in 1971 to weakly impose Dirichlet conditions without having to add Lagrange multipliers. To implement the continuity condition by the Nitsche method, one can, following for example Ref. 4, start from the weak form of a generic boundary condition
(3-191)
where A(u) is a flux-like operator and B(u) is a trace-like operator that can be seen as a conjugate pair, and δ represents the test function. The next step is to reformulate these operators as
where c is a known quantity such as a prescribed displacement, γ is a stabilization factor, and θ is a parameter used to control the symmetry of the formulation. Inserting these reformulations of A(u) and B(u) into Equation 3-191, after simplification, leads to the following weak contribution for implementing the Nitsche method for a generic boundary condition
To implement the continuity condition the unknowns A(u), B(u), and c has to be identified. Considering the continuity of displacements in Equation 3-189, the displacement jump across the interface is defined as
By also using the average traction defined as
the action-reaction principle in Equation 3-190 can be weakly imposed as
From the above and Equation 3-191, it can identify that
and one can also realize that for continuity, c = 0. The Nitsche formulation of the continuity conditions then follows as
From the above weak equation several variants of the Nitsche formulation can then be set up. Firstly, it is possible to parameterize the integrals on both sides of the interface, or alternatively on either Γsrc or Γdst only. The first option is less sensitive to the mesh on either side, but can be more expensive since it involves more mapping operations to evaluate. Secondly, the parameter θ makes it possible to set up formulations with different properties and stability:
•
Setting θ = 1 results in a symmetric formulation that maintains the symmetry of the overall system of equations. The main drawback of this setting is that is requires a suitable choice for γ to maintain accuracy and stability.
•
Setting θ = −1 results in a skew-symmetric formulation. This formulation is much less sensitive to the choice of γ, but makes the overall system of equations nonsymmetric.
•
Setting θ = 0 results in an incomplete formulation. This formulation is less sensitive to the choice of γ than the symmetric one, but not as robust as the skew-symmetric. However, this choice causes the term δTavg to cancel out. For large deformations and nonlinear materials in particular, this term can be expensive to evaluate, making the nonsymmetric formulation an attractive choice.