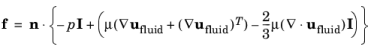Fluid–Structure Interaction multiphysics coupling combines fluid flow with structural mechanics to capture the interaction between the fluid and the solid structure. A structural mechanics interface (Solid Mechanics, Shell, Membrane, or Multibody Dynamics) and a Single-Phase Flow interface model the solid and the fluid, respectively. The Fluid–Structure Interaction (FSI) couplings appear on the boundaries between the fluid and the solid. The physics interface uses an arbitrary Lagrangian-Eulerian (ALE) method to combine the fluid flow formulated using an Eulerian description and a spatial frame with solid mechanics formulated using a Lagrangian description and a material (reference) frame.
The fluid flow is described by the Navier–Stokes equations, which provide a solution for the velocity field ufluid. The total force exerted on the solid boundary by the fluid is the negative of the reaction force on the fluid,
where p denotes pressure,
μ the dynamic viscosity for the fluid,
n the outward normal to the boundary, and
I the identity matrix. Because the Navier–Stokes equations are solved in the spatial (deformed) frame while the structural mechanics interfaces are defined in the material (undeformed) frame, a transformation of the force is necessary. This is done according to
where dv and
dV are the mesh element scale factors for the spatial frame and the material (reference) frame, respectively.
The structural mechanics formulations support geometric nonlinearity (large deformations). The spatial frame also deforms with a mesh deformation that is equal to the displacements ustruct of the solid within the solid domains. The mesh is free to move inside the fluid domains, and it adjusts to the motion of the solid walls. This geometric change of the fluid domain is automatically accounted for in COMSOL Multiphysics by the ALE method.
For small values of the structural displacement and its rate of change, the Fluid–Structure Interaction interface includes one-way model formulations. The one-way models sequentially solve for the fluid flow, compute the load from Equation 3-180, and then apply it in the solution for the solid displacement. Since these methods are unidirectional, the mesh deformation is excluded from the solution. When applicable, the one-way versions offer computationally cheaper alternatives to a fully coupled counterpart.
In this case the one-way study steps display under Preset Studies for Some Physics Interfaces branch since the Fluid study step does not solve for the solid displacement and vice versa. When using a turbulence model requiring the distance to the closest wall, the Preset Studies includes a
Wall Distance Initialization study step.