Without loss of generality, consider waves propagating along the x-axis. The waves are linear, so that small strains are assumed.
where K and
G are the bulk and shear moduli, respectively; and
ηb and
ηv are the bulk and shear viscosity coefficients, respectively.
The shear waves are solutions of the form: 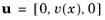 , where the y
, where the y-polarization is assumed, again without loss of generality. The corresponding momentum balance equation is
where U+ and
U- are constant amplitudes, and
For each wave, the spatial attenuation is characterized by α(
ω) which is often called the attenuation coefficient. It has a SI unit (1/m), but is often given using neper per meter (Np/m). Alternatively, the value can be given in decibel per meter (dB/m). Both Np and dB are relative units (dimensionless). Values given in Np or Np/m can be used directly in any formula using SI units. The conversion formula needs to be applied for values using dB:
For given values of attenuation coefficients αp and
αs measured in Np/m at the corresponding references frequencies
fp,ref and
fs,ref the approximate formulas for the viscosity coefficients are
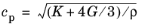 and
and 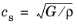 . If the values of αp
. If the values of αp and
αs are given in dB/m, the conversion factor ln(10)/20 needs to be inserted.