Magnetostriction describes the change in dimensions of a material due to a change in its magnetization. This phenomenon is a manifestation of magnetoelastic coupling, which is exhibited by all magnetic materials to some extent. The effects related to magnetoelastic coupling are described by various names. The Joule effect describes the change in length due to a change in the magnetization state of the material. This magnetostrictive effect is used in transducers for applications in sonars, acoustic devices, active vibration control, position control, and fuel injection systems.

The inverse effect accounts for the change in magnetization due to mechanical stress in the material. This effect is also known Villari effect. This effect is mostly useful in sensors.

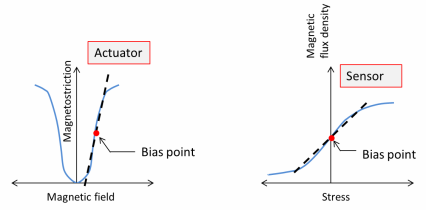
It is possible to express the relation between the stress S, strain ε, magnetic field H, and magnetic flux density B in either a stress-magnetization form or strain-magnetization form:

where μ0 is the magnetic permeability of free space; cH and sH are the stiffness and compliance matrices measured at constant magnetic field, respectively; and μrS and μrT are the relative magnetic permeabilities measured at constant strain and constant stress, respectively. The matrices dHT and eHS are called piezomagnetic coupling matrices.

All the necessary material data inputs are placed within the Piezomagnetic Material node under the Solid Mechanics interface, which are added automatically when adding a predefined Piezomagnetism multiphysics interface. Such a node can be also added manually under any Solid Mechanics interface similar to all other material model features. The Piezomagnetic Material uses Voigt notation for the anisotropic material data. More details about the data ordering can be found in the Orthotropic and Anisotropic Materials section.

The following material data corresponds to Terfenol-D at 100 kA/m bias and 30 MPa prestress (Ref. 6):

The strain tensor C, the magnetic field H, and the temperature T are used as the state variables. The free energy density in the undeformed configuration is defined as

where c is the elasticity tensor.

where Hs and H are the magnetic fields in the deformed (spatial) and undeformed configuration, respectively.

The Maxwell stress SM is related to the magnetization of the free space occupied by the deformed body, and it is computed as

The piezomagnetic strain tensor is introduced as 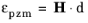, where d is the piezomagnetic coupling tensor. The piezomagnetic deformation gradient is modeled as

which are the strain and stress tensors in the intermediate configuration, where the thermal expansion part have been removed. These quantities are independent of the magnetic field H.

where μr is the relative magnetic permeability.

A commonly accepted micromagnetic description of the magnetostriction is as follows (Ref. 2):

All domains have magnetization of the same magnitude |M| = Ms, but the magnetization can have different orientations characterized by the corresponding direction vector m = M/Ms for each domain. The applied magnetic field changes the domain orientation.

where 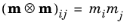. Note that the magnetostrictive strain is represented by a deviatoric tensor, thus tr(εme) = 0. This is because the deformation is related to the magnetic domain rotation, and such process should not change the material volume.

The strain in any direction given by the directional cosines βi can be written as

Using Equation 3-153, one gets

When both magnetization and measurement direction are parallel to the same crystal direction [100], one has m1 = β1 = 1 and all other components are zero, so that

In a similar way for the [111] direction, one has for all components and λ = λ111.

If the strain is measured in [100] direction, while all the magnetization vectors are aligned perpendicular to it, one has only the following two nonzero components: m2 = β1 = 1 and consequently:

For an isotropic material, λ100 = λ111 = λs, and Equation 3-153 becomes

For a polycrystalline material without preferred orientation, the following approximation can be used (Ref. 1):

The strain field is deviatoric, and Equation 3-155 exhibits the same properties as Equation 3-153 at saturation, that is, when |M| → Ms. Equation 3-154 is replaced by

Note that the strain vanishes when |M| → 0, which makes the model applicable in the whole range from full demagnetization to saturation.

For isotropic materials, the magnetostrictive strain is modeled as the following quadratic isotropic form of the magnetization field using tensor notation (Ref. 3):

where cH is a 6-by-6 stiffness matrix. For isotropic materials, the matrix can be represented in terms of two parameters, for example, using the Young’s modulus and Poisson’s ratio. Cubic materials possess only three independent components: c11, c12, and c44.

One can derive a linear response around a given bias state characterized by a premagnetization vector M0. Thus,

where M1 is a perturbation.

Using Equation 3-156,one finds

The magnetization in the magnetostrictive material is found from the following nonlinear implicit relation (Ref. 4 and Ref. 5):

where L is the Langevin function

with χ0 being the magnetic susceptibility in the initial linear region.

Other possible choices of the L function are a hyperbolic tangent, which is sometimes referred to as the Ising model

where H is the applied magnetic field. The second term in Equation 3-158 represents the mechanical stress contribution to the effective magnetic field, and thus to the material magnetization, which is called the Villari effect. The deviatoric stress tensor is related to the strain as

In addition, the magnetization and magnetic field are related to each other and to the magnetic flux density (also called the B-field) by

COMSOL Multiphysics solves for the magnetic vector potential A whose curl yields the vector B-field. The H-field is then obtained as a function of the B-field and magnetization

is the tangent magnetic susceptibility. The corresponding expression in case of cubic material is more complicated, but it has a similar structure involving products of the magnetization and tangent susceptibility components. An important observation from the above formulas is that the piezomagnetic coefficients should reach their maximum (or minimum) at certain strength of the applied bias field if the saturation effect is taken into account. This is because M is zero at zero applied field, while χm tends to zero at large applied field magnitudes because of saturation.

The piezomagnetic coupling tensor d is a third order tensor. Due to the symmetry, it can be conventionally represented by a 3-by-6 matrix dHT with only few nonzero components.

The Jiles–Atherton hysteresis model for magnetostrictive materials is available COMSOL Multiphysics. The model assumes that the total magnetization can be represented as a sum of hysteretic and anhysteretic parts, the latter one is given by Equation 3-157, thus

Compared to Equation 3-158 and Equation 3-159, the effective magnetic field Heff gets one more term αM, where α is the interdomain coupling parameter.

where cr is the reversibility parameter, and kp is the pining loss parameter.

Equation 3-160 can be solved using either a time-dependent analysis or a stationary parametric sweep.