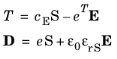The direct  piezoelectric effect consists of an electric polarization in a fixed direction when the piezoelectric crystal is deformed. The polarization is proportional to the deformation and causes an electric potential difference over the crystal.

The inverse piezoelectric effect, on the other hand, constitutes the opposite of the direct effect. This means that an applied potential difference induces a deformation of the crystal.

It is possible to express the relation between the stress, strain, electric field, and electric displacement field in either a stress-charge form or strain-charge form:

In the above relations, the naming convention used in piezoelectricity theory is assumed, so that the structural strain is denoted by S, and the stress is denoted by T. Thus, the naming convention differs in piezoelectricity theory compared to structural mechanics theory.

All the necessary material data inputs are placed within the Piezoelectric Material feature under the Solid Mechanics interface, which are added automatically when adding a predefined Piezoelectricity multiphysics interface. Such node can be also added manually under any Solid Mechanics interface similar to all other material model features. The piezoelectric material uses the Voigt notation for the anisotropic material data, as customary in this field. More details about the data ordering can be found in Orthotropic and Anisotropic Materials section.

The equations of Piezoelectricity combine the momentum equation Equation 3-166 with the charge conservation equation of Electrostatics,

where the ρV is the electric charge concentration. The electric field is computed from the electric potential V as

In both Equation 3-149 and Equation 3-166, the constitutive relations Equation 3-146 are used, which makes the resulting system of equations closed. The dependent variables are the structural displacement vector u and the electric potential V.

In case of geometric linearity, the governing equations for a linear piezoelectric medium of any anisotropy can be written in terms of the structural displacement vector u and electric potential V as:

Since the relations in Equation 3-150 are linear, they possess the following time-harmonic wave solutions:

where k = kn is the wave number vector, n is the direction vector that defines the wavefront propagation direction. The wavefront is an imaginary line connecting solid particles of the same phase. The velocity of such wavefront in the direction normal to it is given by the phase velocity c = ω/k.

A generalization of Christoffel’s equation (Equation 3-25) can then be done:

which is called the dispersion relation. This is in general case a cubic polynomial in terms of c2, which has three roots . Thus, for an arbitrary anisotropic medium, three waves with different phase velocities can propagate in each given direction.

For example, the pressure wave propagating in the X direction is a particular solution, for which

The shear wave propagation in the X direction and with XY-plane polarization is a solution such that

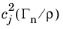
where un,j is the wave polarization vector that is the eigenvector corresponding to the eigenvalue solution of the Christoffel’s equation.

COMSOL Multiphysics provides predefined variables for the phase and group velocities for waves of different types propagating in any chosen direction. These variables do not affect the solution as such, but are available during result presentation if the Wave Speeds node has been added to the material.

Complex-valued data can be defined directly in the fields for the material properties, or a real-valued material X and a set of loss factors ηX can be defined, which together form the complex-valued material data

For these cases, it is thus necessary that ηX is positive in order for the material to be thermodynamically stable with the chosen signs.

The sign of the coupling losses requires more considerations, and the chosen sign must be considered as a definition. All values of ηe and ηd does not necessarily have to be positive. For some simple theoretical cases with isotropic loss factors, it can however be shown that the definition above is reasonable:

It is also possible to define the electrical conductivity of the piezoelectric material, σ. Electrical conductivity appears as an additional term in the variational formulation (weak equation form). The conductivity does not change during transformation between the formulations.

Using the functionality available under the Piezoelectric Material feature and Solid Mechanics interface, one can define initial stress (S0), initial strain (ε0), and remanent electric displacement (Dr) for models. In the constitutive relation for piezoelectric material these additions appear in the stress-charge formulation:

The strain tensor C, the electric field E, and the temperature T are used as the state variables. The free energy density in the undeformed configuration is defined as

where c is the elasticity tensor.

where Es and E are the electric fields in the deformed (spatial) and undeformed configuration, respectively.

The Maxwell stress SM is related to the polarization of the free space occupied by the deformed body, and it is computed as

The piezoelectric strain tensor is introduced as 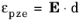, where d is the piezoelectric coupling tensor. The piezoelectric deformation gradient is modeled as

which are the strain and stress tensors in the intermediate configuration, where the thermal expansion part have been removed. These quantities are independent of the electric field E.

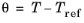
where εr is the relative electric permittivity, p is the pyroelectric coefficient, and is the temperature variation.