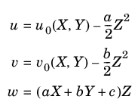One possible extension of the Plane Strain formulation is to assume that the displacement field depends on the out-of-plane coordinate Z, but in-plane strains are independent of it.

here, u0(X,Y) and v0(X,Y) are the in-plane displacement components; and a, b, and c are constants independent of the X, Y, and Z coordinates. The gradient of the displacement field then reads:

At the cross section Z = 0, the in-plane deformation is fully characterized by the in-plane displacement components u0(X,Y) and v0(X,Y). The displacement gradient then simplifies to

The out-of-plane shear strains are zero, εxz = εyz = 0, and under the assumption of small displacements and rotations the normal strain reads

The above conditions differ from the Plane Strain formulation only by the fact that the out-of-plane strain component εz can vary linearly throughout the cross section.

The generalized plane strain approximation is good when the structure is free to expand in the out-of-plane direction, and the possible bending curvature is small with respect to the extents of the structure in the xy-plane. In the case where there is no out-of-plane bending, the out-of-plane strain component simplifies to εz = c.

In COMSOL Multiphysics, the coefficients a, b, and c in Equation 3-8 are modeled as extra degrees of freedom that are constant throughout the model (global variables).

For the 1D representation, only the x-component of the displacement field is considered, and only gradients with respect to this direction are computed, this is, u = u(X), ∂u/∂Y = ∂u/∂Z = 0, and εxy = εy = 0. It is possible to apply the generalized plane strain assumption to either the xy-plane, the xz-plane, or to both planes, in which case the strain components are augmented to εy = b and εz = c.

For the 1D axisymmetric representation, only the radial component of the displacement field is considered, and only gradients with respect to this direction are computed, this is, u = u(R), and ∂u/∂Φ = ∂u/∂Z = 0. It is possible to apply the generalized plane strain assumption to the rϕ-plane, so the strain is augmented to εz = c.

Coefficients a, b, and c are assumed to be small. Then, using the above displacement field in the displacement gradient evaluated in the plane Z = 0 simplifies to

We obtain the strain components by dropping quadratic and higher order terms in the coefficients a, b, and c:

Thus, in the leading order approximation, the strains become independent of the out-of-plane coordinate Z.

When a 2D plane strain model represents a cross-section of the structure that has a significant uniform extension in the out-of-plane Z direction, the following 3D solution can be sought in form of the amplitude expansion:

The first term, u0, represents a static in-plane prestress deformation:

The second part of the solution, u1, presents a time-harmonic linear perturbation with an amplitude that can be a function of the in-plane coordinates X and Y. Such a perturbation can be seen as an out-of-plane wave, with a small amplitude that propagates in the Z direction, a wavelength L, and phase velocity c:

Note that in contrast to the prestress solution u0, the perturbation amplitude u1 can have nonzero values in all the displacement components:

There are two alternative approaches. The wavelength L, and thus the wave number kZ, can be considered as a parameter. Then, ω can be computed by an eigenfrequency analysis for the 2D cross section with all three displacement components taken as dependent variables. As a result, one obtains

Thus, the wave speed for the out-of-plane wave is computed as a function of the wavelength L and possible prestress u0 in the material. The dependence of the wave speed on the wavelength is often called dispersion.

Alternatively, the frequency f (and thus ω) can be taken as a parameter. Then, the solution can be computed via eigenvalue analysis with respect to the wave number kZ using the 2D cross section geometry. Hence,

which determine the wavelength L and phase velocity c for the wave that propagates out-of-plane for a given frequency f under given in-plane prestress deformation u0. Such interpretation of the perturbation solution is sometimes called a signaling problem.