Lagrangian Formulation

The formulation used for structural analysis in COMSOL Multiphysics for both small and finite deformations is a total Lagrangian formulation. This means that the computed stress and deformation state is always referred to the material configuration rather than to current position in space.

Likewise, material properties are always given for material particles and with tensor components referring to a coordinate system based on the material frame. This has the obvious advantage that spatially varying material properties can be evaluated just once for the initial material configuration, and they do not change as the solid deforms and rotates.

Consider a certain physical particle, initially located at the coordinate X. During deformation, this particle follows a path

Here, x is the spatial coordinate and X is the material coordinate.

For simplicity, assume that undeformed and deformed positions are measured in the same coordinate system. Using the displacement u it is then possible to write

The displacement is considered as a function of the material coordinates (X, Y, Z), but it is not explicitly a function of the spatial coordinates (x, y, z). It is thus only possible to compute derivatives with respect to the material coordinates.

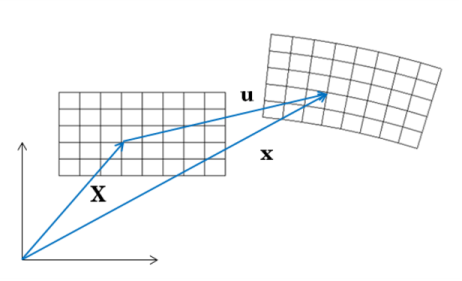
In the following, the gradient operator is assumed to be a gradient with respect to the material coordinates, unless something else is explicitly stated.

The gradient of the displacement, which occurs frequently in the following theory, is always computed with respect to material coordinates. In 3D:

The deformation gradient tensor, F, shows how an infinitesimal line element, dX, is mapped to the corresponding deformed line element dx by

The deformation gradient F contains the complete information about the local straining and rotation of the material. It is a two-point tensor (or a double vector), which transforms as a vector with respect to each of its indices. It involves both the reference and present configurations.

In terms of the displacement gradient, F can be written as

The deformation of the material (stretching) will in general cause changes in the material density. The ratio between current and initial volume (or mass density) is given by

Here, ρ0 is the initial density and ρ is the current density after deformation. The determinant of the deformation gradient tensor F is related to volumetric changes with respect to the initial state. A pure rigid body displacement implies J = 1. Also, an incompressible material is represented by J = 1. These are called isochoric processes.

The determinant of the deformation gradient tensor is always positive (since a negative mass density is unphysical). The relation ρ = ρ0/J implies that for J < 1 there is compression, and for J > 1 there is expansion. Since J > 0, the deformation gradient F is invertible.

In the material formulations used within the structural mechanics interfaces, the mass density should in general be constant because the equations are formulated for fixed material particles. Thus, do not use temperature-dependent material data for the mass density. The changes in volume caused by temperature changes are incorporated using the coefficient of thermal expansion when adding Thermal Expansion (for Materials) to the material model.