Effects of Internal Pressure
Hoop Stress
When an internal pressure is present in a pipe, it must be balanced by a net force in the circumferential direction. For a circular pipe, this stress component is often called hoop stress. For a thin-walled circular pipe, it is given by the well-known expression
where p is the pressure, R is the radius of the pipe, and t is the wall thickness.
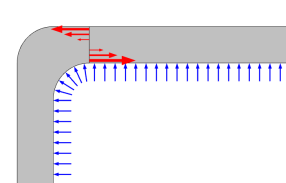
The pressure p here is the gauge pressure, assumed to be positive. If the pressure in the pipe is given as an absolute pressure, then the external pressure (usually 1 atm) must also be supplied. It is assumed that the external pressure is small relative to the internal pressure, so that the stress distribution through the pipe wall is given only by the gauge pressure p = pinternal - pexternal.
In particular, the Pipe Flow interface operates with absolute pressures, so when running a combined analysis, it is important to include also the external pressure.
For stress evaluation in a general cross section, the average (or membrane) hoop stress can be written as
where γm is a dimensionless factor multiplying the pressure.
The average hoop stress is available in the variable pipem.shm.
For a general thick-walled circular pipe, the average hoop stress is given by
where the inner and outer diameters have been introduced.
For a thick circular pipe, the hoop stress may however have a significant variation through the thickness (Figure 12-1).
Figure 12-1: Hoop stress distribution in a thick-walled pipe.
The peak circumferential stress is
The difference between the peak circumferential stress and the mean circumferential stress is
Here, γb is a cross section dependent factor, which is used to compute the peak stress due to internal pressure.
The bending part of the hoop stress is available in the variable pipem.shb.
For noncircular pipe sections, the nonuniform stress distribution is more prominent. For such sections, the bending stress in the pipe wall can be much larger than the mean stress which balances the internal pressure. This is indicated in Figure 12-2.
Figure 12-2: Bending stress caused by internal pressure in rectangular pipe section.
For a rectangular pipe section, the bending stress can be estimated using beam theory. If the cross section is considered as a rectangular frame with constant thickness t, then the moment (per unit length) at the corner will be
Here, the length in the horizontal direction is Ly and the length in the vertical direction is Lz.
The nominal bending stress at the corner is thus
The bending part of the hoop stress is available in the variable pipem.shb.
For normal values of wall thickness to section width ratios and corner fillet radii, this will give a good approximation.
The average stress, which is given by the force balance, is
The average hoop stress is available in the variable pipem.shm.
Thus,
For rectangular pipe sections, the bending stress is thus always larger than the membrane stress.
Poisson’s Ratio Effect
Due to the stresses and corresponding strains in the circumferential direction, there will be a coupling to axial deformation through Poisson’s ratio. The bending stresses within the pipe wall are self-equilibrating and does not have a net effect. For a cylindrical pipe, it can be shown that the radial and hoop stresses together cause a homogeneous axial strain throughout the wall. Thus, no local axial stresses are introduced. For a general cross section, the local axial stress caused by is assumed to be
The axial stress contribution from the bending part of the hoop stress is available in the variable pipem.shbn.
The average hoop stress will, however, always cause an axial strain. Since the diameter of the pipe increases under an internal pressure, the pipe must, if the ends are free, contract. Equivalently, if the ends of the pipe are kept fixed, a tensile axial force is introduced. It can be shown that for any pipe cross section, this force is
where Af is the cross-section area of the fluid. Note that the force is independent of the geometry of the wall itself.
The corresponding axial strain in the case of free axial deformation is
This term is added as an initial strain to the constitutive relation.