|
•
|
In 3D, you must specify the x2 direction and thus implicitly the x3 direction. You specify the orientation either by selecting a point in the x1-x2 plane or by defining an orientation vector in an approximate x2 direction. In either case, the actual x2 direction is chosen so that it is perpendicular to the SCL and lies in the plane you have specified. The x3 orientation is then taken as perpendicular to x1 and x2. As long as you are only interested in a stress intensity, the choice of orientation is arbitrary.
|
|
•
|
In 2D, the x3 direction is the out-of-plane direction, and the x2 direction is perpendicular to the SCL in the XY-plane.
|
|
•
|
In 2D axial symmetry, the x3 direction is the azimuthal direction, and the x2 direction is perpendicular to the SCL in the RZ-plane.
|
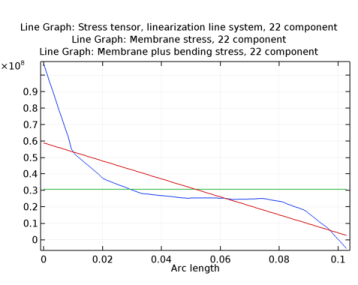
|
Sllsij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Smij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Sbmaxij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Sbij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Smbij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Spsij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Speij
|
ij = 11, 12, 13, 22, 23, 33
|
|||
|
Nij
|
ij = 22, 23, 33
|
|||
|
Mij
|
ij = 22, 23, 33
|
|||
|
Qi
|
i = 2, 3
|
|||
|
Stress Linearization in the Structural Mechanics Theory chapter.
|