The thickness of the membrane is d, which can vary over the element. The displacements are interpolated by Lagrange or Serendipity shape functions.

This local membrane surface coordinate system is defined by the boundary coordinate system (tl, t2, n).

Many features, such as an edge load, allow input in an edge local coordinate system. The orthogonal local edge coordinate system directions xl, yl, and zl are defined so that:

The local edge system can be visualized by plotting the components of the local edge transformation matrix with an Arrow Line plot. The matrix components are defined per feature. For instance, the variable name for the xx-component is <interface>.<feature_tag>.TleXX.

When an edge is shared between two or more boundaries, the directions may not always be unique. It is then possible to use the control Face Defining the Local Orientations to select from which boundary the normal direction zl should be picked. The default is Use face with lowest number.

If the geometry selection contains several edges, the only available option is Use face with lowest number, since the list of adjacent boundaries would then be different for each edge. For each edge in the selection, the face with the lowest number attached to that edge is then used for the definition of the normal orientation.

The deformation gradient F is in general defined as the gradient of the current coordinates with respect to the original coordinates:

Here ∇tu is the displacement gradient computed using the tangential gradient on the membrane surface, and N is the normal vector to the undeformed membrane. The tangential deformation gradient Ft then contains information about the stretching in the membrane plane.

Since the tangential deformation gradient does not contain any information about the transverse (out-of-plane) stretch λn, it must be augmented by the normal deformation gradient Fn to define the full deformation gradient. It is given by

where n is the normal vector to the deformed membrane. For anisotropic materials, the shear deformation gradient Fs is also needed to define the full deformation gradient. It is given by

where t1 and t2 are the tangent vectors on the deformed membrane surface. The full deformation gradient F is then computed from the sum of tangential, shear, and normal deformation

Note that Fs is only nonzero for anisotropic materials, otherwise Fs = 0.

The right Cauchy–Green tensor C is then defined as

The Jacobian J is the ratio between the current volume and the initial volume. In full 3D it is defined as

When using the traditional membrane theory, which does not incorporates a wrinkling model, negative principal stresses result in an equilibrium instability. In order to overcome this instability, the wrinkling model within the framework of the tension field theory can remove compressive stresses from wrinkled regions resulting in a correct stress distribution, Ref. 1–3.

The modified membrane theory, which incorporates a wrinkling model to the traditional membrane theory, disregards the out-of-plane deformation in wrinkling; so wrinkles including details like their amplitude and wavelength are determined on the mean surface of the membrane (Ref. 1–3).

There are two approaches to embed the tension field theory into the framework of classical membrane theory, but essentially both approaches are equivalent (Ref. 3). One approach is to replace the strain energy density with a relaxed variant of it, while the other approach is to modify the deformation gradient (Ref. 1). While the first approach can only be used for isotropic membranes, the second approach is more general (Ref. 1), and it is the method implemented in COMSOL Multiphysics.

The undeformed configuration of the membrane is described by the material coordinates X, Y, and Z. The uniaxial stress occurs in the X direction; Y is the wrinkling direction and Z is the normal to the membrane plane (Figure 7-1). The deformed configuration is represented by the x, y, and z coordinates. After deformation, the membrane can be in one of three possible states:

As shown in Figure 7-1 there are three different kinematic descriptions (Ref. 1):

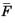
When n1 is the direction of uniaxial extension, and assuming that wrinkling occurs in the n2 direction, the modified deformation tensor is written as

Here, β is the wrinkling parameter, so β = 0 represents a taut condition. According to the orthogonality condition in tension field theory, these two vectors satisfy

where σ is the Cauchy stress tensor written in terms of the second Piola–Kirchhoff stress tensor

Assuming that the mean configuration F is known, the only unknowns in Equation 7-1 and Equation 7-2 are β and n2.

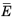
Since the material properties and membrane theory itself are given in the reference configuration, Equation 7-1 and Equation 7-2 are transformed to the reference configuration (Ref. 2). The fictive Green–Lagrange strain tensor is then written with the help of a vector in the reference configuration which corresponds to the wrinkling direction n2, so g = n2⋅F,

where βm and N2 are the wrinkling parameter and wrinkling direction in the reference configuration. The two unknowns β and n2 in the deformed configuration are replaced by the two unknowns βm and N2 in the reference configuration.

The membrane surface is spanned by a coordinate system having two in-plane orthogonal unit vectors e1 and e2. Thus, N1 and N2 can be written with the help of the wrinkling angle αm

So the scalar wrinkling angle αm is sufficient to define the wrinkling vector N2. The two nonlinear equations in Equation 7-2 are then solved for the two unknowns αm and βm with the Newton-Raphson method. Once the parameters αm and βm are determined, the deformation gradient and the second Piola–Kirchhoff stress tensor are modified to get the correct stress distribution and to define the wrinkled regions.

where the force F can be distributed over a boundary, an edge, or it can be concentrated in a point. In the special case of a follower load, defined by a pressure p, the force intensity is F = −pn, where n is the normal vector to the membrane surface in the deformed configuration.