Shape Functions
The beam element has different shape functions for representing the displacements in different directions.
•
The axial extension is represented by a linear shape function.
•
The twist around the beam axis (3D only) is represented by a linear shape function.
•
The bending displacement and corresponding rotation are represented by cubic shape functions, usually called Hermitian shape functions. These will supply exact solutions to the underlying beam equations as long as distributed loads do not vary with position.
The shape functions for bending depend on whether Timoshenko theory is employed or not.
In the beam local system, the displacements, u, and rotations, θ, are interpolated as
where the subscript refers to the two nodes of the element, and N is a matrix of shape functions.
The shape functions for the Euler-Bernoulli case are expressed in the local coordinate ξ, ranging from 0 to 1, as
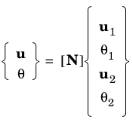
where L is the length of the beam element.
For the Timoshenko case, the shape functions are modified, so that they depend on the degree of shear flexibility. Define
which represent the ratios between bending and shear stiffness in the two principal directions. The shape functions are then modified so that
where
The superscript i indicates that the shape functions for bending are no longer the same in the two principal directions. The shape functions with i = 2 are used for bending in the local y direction, and the shape functions with i = 3 are used for bending in the local z direction.