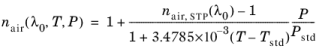The Refractive index, real part, n (dimensionless) may be expressed as a function of wavelength using an optical dispersion model. The Optical dispersion model for domains outside the selection can be specified in the Geometrical Optics interface. Domains that are included in the Geometrical Optics interface selection have dispersion models that are specified in the Medium Properties feature.

A dispersion model for the refractive index of air can be used in exterior and unmeshed domains. It can also be used to convert from relative to absolute refractive indices (see below). The Edlén (1953) air model, described in Ref. 2, which gives the refractive index of air nair as a function of wavelength, temperature, and pressure is

where T is the temperature (SI unit: K) and P is the pressure (SI unit: Pa). The refractive index of air at standard temperature and pressure, nair,STP, is given by

where, by definition, the standard temperature is Tstd = 15°C and the standard pressure is Pstd = 101,325 Pa (and with a CO2 concentration of 0.03%) with the wavelength given in microns; that is λ′ = λ/1[μm].

It is important to appreciate that the refractive indices given by manufacturers are often relative to air at a certain temperature and pressure. Therefore, each of the optical dispersion models (except Temperature-dependent Sellmeier) require a reference temperature Tref (SI unit: K) and pressure Pref (SI unit: Pa) to be specified. This is interpreted to be the temperature and pressure of the air in which the refractive indices used to generate the model were measured. The reference pressure is absolute. If the reference pressure Pref ≠ 0, then it is assumed that the dispersion model will give relative refractive indices nrel (dimensionless). The conversion of refractive index from relative (nrel) to absolute (n) is made using a model for the refractive index of air (nair). That is,

with nair defined in Equation 3-5 with T = Tref and P = Pref.

Each model requires a set of coefficients to be specified. These can be determined, for example, by making a least squares fit to a set of refractive index measurements at discrete wavelengths. At least one optical dispersion model (Temperature-dependent Sellmeier) allows the refractive index to be expressed as a function of both wavelength and temperature. All other optical dispersion models may be used together with a thermo-optic dispersion model to calculate a temperature-dependent shift in the refractive index. This is discussed in Thermo-Optic Dispersion Models.

The built-in optical dispersion models are listed in Table 3-3.

All optical dispersion models assume that coefficients have been determined with expressions where the wavelengths have units of μm. For example, in the Schott model, the coefficients have units 1, μm, μm2, μm3, and so on. The input wavelength can still have any unit; the normalization to microns is done automatically.

The Temperature-dependent Sellmeier model (Ref. 3, Ref. 4) assumes coefficients based on absolute temperature specified in Kelvin (K).