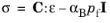
Here, σ is the Cauchy stress tensor, ε is the strain tensor, αB is the Biot–Willis coefficient, and pf is the fluid pore pressure. For linear elasticity, the coefficients in the elasticity matrix C must be measured under “drained” conditions by measuring the strain induced by a change in stress (or by measuring the induced stress by changes in strain) under constant pore pressure.

where Gd is the shear modulus of the drained porous matrix.

The volumetric coupling is derived by taking the trace of the stress tensor σ, as written in Equation 7-1

Here, the mean pressure pm is positive in compression, Kd is the bulk modulus of the drained porous matrix, and the volumetric strain εvol is a measurement of the porous matrix dilation or contraction (negative in compression).

Note that the Poroelasticity multiphysics coupling adds the contribution from the pore pressure,  αBpf, as a load. In this setting, the variables for the stress tensor σ and mean pressure pm are effective stress measures.

The other constitutive relation in Biot’s theory of poroelasticity (Ref. 1) relates the increment in fluid content ζ to changes in volumetric strain and pore pressure. The pore pressure is proportional to the dilation of the porous matrix and the variation in fluid content:

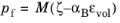
Biot and Willis (Ref. 1) measured the coefficients αB and M with the unjacketed compressibility test and derived expressions for these coefficients in terms of solid and fluid bulk moduli (or compressibilities).

The variable M, sometimes called the Biot modulus, is the inverse of the storage coefficient Sp in the Darcy’s law interface. It is defined through Equation 7-2 as the change in fluid content due to changes in pore pressure under constant deformation (constant volumetric strain):

Using this definition, it is possible to measure the storage coefficient Sp directly in the lab, and, in the case of an ideal isotropic porous material, it can be calculated from basic material properties as

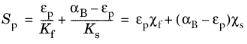
where εp is the initial porosity, Kf the fluid bulk modulus (the inverse of the fluid compressibility χf), and Ks the solid bulk modulus (the inverse of the solid compressibility χs); that is, the theoretical bulk modulus of a homogeneous block of the solid material making up the porous matrix.

The Biot–Willis coefficient, αB, relates the volume of fluid expelled (or sucked into) a porous material element due to the volumetric change of the same element. This coefficient can be measured experimentally as the change in mean pressure due to changes in the pore pressure under constant deformation (constant volumetric strain). In the case of an ideal isotropic porous material it can be defined in terms of the drained and solid bulk moduli as

The drained bulk modulus Kd is always smaller than the solid bulk modulus Ks (a solid block is stiffer than a porous block made of the same material), and therefore the Biot–Willis coefficient is bounded to εp ≤ αB ≤ 1.

The Biot–Willis coefficient depends on the properties of the porous matrix but not on the properties of the fluid. A soft porous matrix is represented by a Biot–Willis coefficient close to unit (since Kd << Ks), while for a stiff matrix, αB is close to the porosity εp, since Kd ≈ (1 − εp)Ks.

By replacing Ks = Kd/(1 − αB), the storage coefficient Sp in Equation 7-3 is calculated in terms of the porosity εp, the Biot–Willis coefficient αB, and the bulk moduli of the fluid Kf and the drained porous matrix Kd as

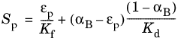
For a soft porous matrix, αB ≈ 1, or for a stiff porous matrix, αB ≈ εp, the lower bound for the poroelastic storage is Sp ≈ εp/Kf.

A special case of Biot’s theory of poroelasticity arises if both the solid and the fluid phases are assumed incompressible. In this case, it follows that χf = χs = 0, the Biot–Willis coefficient αB = 1, and the storage coefficient Sp = 0. The corresponding governing equations are then identical to those derived for a biphasic porous medium with incompressible solid and fluid constituents (Ref. 3). This version of the poroelasticity coupling is available by selecting the Biphasic poroelasticity model, see Poroelastic Coupling Properties.

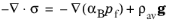
where σ is the stress tensor computed from linear elasticity, and g is the gravitational acceleration. The average density ρav is computed from

where ρf represents the fluid density, ρd = (1 − εp)ρs the density of the dry porous matrix, and ρs the density of the solid material.

The fluid-to-structure coupling enters as an additional volumetric force in the momentum equation as described in Equation 7-5, which can be identified as an external load due to the fluid pressure, see External Stress in the Structural Mechanics Module User’s Guide for details.

Equation 7-5, which describes an equilibrium state (inertial effects are neglected), also applies to the case of a time-dependent flow model. This is a valid assumption in geotechnical and biological applications since the time scale of the inertial response is generally many orders of magnitude faster than the time scale of the flow. When you study the coupled process on the time scale of the flow, you can therefore assume that the solid reaches a new equilibrium immediately in response to a change in the flow conditions. This means that the stresses and strains change in time — even if Equation 7-5 appears to be stationary — and that the structure-to-fluid coupling term, involving the rate of strain, is nonzero.

When Include inertial terms is selected, the average density is used in the inertial term for the momentum equation. In the presence of a volume force f (for example, gravity), the momentum balance then reads

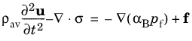
where u represents the solid displacement and ρav the average density.

Inertial effects are also included when modeling waves in saturated porous media, see the Theory for the Poroelastic Waves Interfaces section in the Acoustics Module User’s Guide for details.