COMSOL 6.2 - Numerical Stability — Stabilization Techniques for Fluid Flow

The momentum equation (Equation 3-10 or Equation 3-12) is a (nonlinear) convection-diffusion equation. Such equations can easily become unstable if discretized using the Galerkin finite element method. Stabilized finite element methods are usually necessary in order to obtain physical solutions. The stabilization settings are found in the main Fluid Flow interface features. To display this section, click the button (

) and select in the dialog box.

There are three types of stabilization methods available for Navier–Stokes — streamline diffusion, crosswind diffusion, and isotropic diffusion. Streamline diffusion and crosswind diffusion are consistent stabilization methods, whereas isotropic diffusion is an inconsistent stabilization method.

For optimal functionality, the exact weak formulations of and constants in the streamline diffusion and crosswind diffusion methods depend on the order of the shape functions (basis functions) for the elements. The values of constants in the streamline diffusion and crosswind diffusion methods follow Ref. 5 and Ref. 6.

For strongly coupled systems of equations, the streamline diffusion method must be applied to the system as a whole rather than to each equation separately. These ideas were first explored by Hughes and Mallet (Ref. 8) and were later extended to Galerkin least-squares (GLS) applied to the Navier–Stokes equations (Ref. 9). This is the streamline diffusion formulation that COMSOL Multiphysics supports.

Streamline diffusion is active by default because it is necessary when convection is dominating the flow.

The governing equations for incompressible flow are subject to the Babuška–Brezzi condition, which states that the shape functions (basis functions) for pressure must be of lower order than the shape functions for velocity. If the incompressible Navier–Stokes equations are stabilized by streamline diffusion, it is possible to use equal-order interpolation. Hence, streamline diffusion is necessary when using first-order elements for both velocity and pressure. This applies also if the model is solved using geometric multigrid (either as a solver or as a preconditioner) and at least one multigrid hierarchy level uses linear Lagrange elements.

Crosswind diffusion can also be formulated for systems of equations, and when applied to the Navier–Stokes equations it becomes a shock-capturing operator. COMSOL Multiphysics supports the formulation in Ref. 9 with a shock-capturing viscosity of the Hughes–Mallet type Ref. 8.

Incompressible flows do not contain shock waves, but crosswind diffusion is still useful for introducing extra diffusion in sharp boundary layers and shear layers that otherwise would require a very fine mesh to resolve.

Crosswind diffusion is active by default as it makes it easier to obtain a solution even if the problem is fully resolved by the mesh. Crosswind diffusion also enables the iterative solvers to use inexpensive presmoothers. If crosswind diffusion is deactivated, more expensive preconditioners must be used instead.

The time-scale tensor for time-dependent problems should in theory depend on a time-scale that many references just set to the time-step taken by the time-solver, Δt (see, for example, Ref. 9 and Ref. 10). This simple approach does not, however, necessarily reflect on the actual time-scales in the physics. A typical example is reacting flows where the time step is often guided by fast reactions, while the flow develops relatively slowly. The COMSOL Multiphysics software can therefore replace Δt2 in the time-scale tensor with measures of type

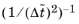
, which are calculated from projections of weak expressions in a fashion similar to those in Ref. 11. These measures of the time scale are used when is activated.

The option can be used to ramp down the time-step contribution in the stabilization when the time step becomes much smaller than the convective and diffusive time scales. This option prevents loss of pressure stabilization at such small time steps.