You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Laminar Flow interfaces provide various predefined inelastic non-Newtonian constitutive models including Power law, Carreau, Carreau–Yasuda, Cross, Cross–Williamson, Sisko, Bingham–Papanastasiou, Herschel–Bulkley–Papanastasiou, Casson–Papanastasiou, DeKee–Turcotte–Papanastasiou, Robertson–Stiff–Papanastasiou, Ellis, and Houska thixotropy.
(3-13)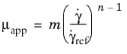
where m,
n are scalars that can be set to arbitrary values and

denotes a reference shear rate for which the default value is 1 s
−1. For
n > 1, the power law describes a shear thickening (dilatant) fluid. For
n < 1, it describes a shear thinning (pseudoplastic) fluid. A value of
n equal to one gives the expression for a
Newtonian fluid.
Equation 3-13 predicts an infinite viscosity at zero shear rate for
n < 1. This is however never the case physically. Instead, most fluids have a constant viscosity for shear rates smaller than 10
−2 s
−1 (
Ref. 17). Since infinite viscosity also makes models using
Equation 3-13 difficult to solve, COMSOL Multiphysics implements the Power law model as
(3-14)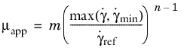
(3-15)
where λ is a parameter with the unit of time,
μ0 is the zero shear rate viscosity,
μ∞ is the infinite shear-rate viscosity, and
n is a dimensionless parameter. This expression is able to describe the viscosity for most stationary polymer flows.
The Carreau–Yasuda model is a generalized version of the Carreau model with the transition parameter a which allows for modifying the stiffness of the transition from constant
μ0 to thinning. So, it has five parameters in the expression:
(3-16)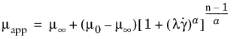
The Cross model is a special case of the Carreau–Yasuda model with a = 1 − n and
λ = μ0/τtr where
τtr is the critical stress. So, it has the following form:
(3-17)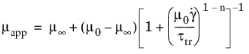
(3-18)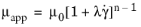
(3-19)
Viscoplastic fluid behavior is characterized by existence of the yield stress τy — a limit which must be exceeded before significant deformation can occur. To model the stress-deformation behavior of viscoplastic materials, different constitutive equations have been propose. The Bingham plastic model is written as
where μp is the plastic viscosity.
(3-20)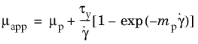
where mp is a scale that controls the exponential growth of stress.
(3-21)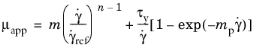
where m,
n are scalars that can be set to arbitrary values, and
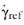
is the reference shear rate. In case
n equals one, the Bingham–Papanastasiou model is recovered. This equation is valid in both yielded and unyielded regions. The exponent
mp controls the smoothness of the viscosity function.
(3-22)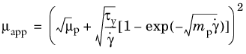
(3-23)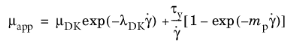
where μDK and
λDK denote the shear rate viscosity and relaxation time respectively. In case
λDK equals zero, it recovers the Bingham–Papanastasiou model.
(3-24)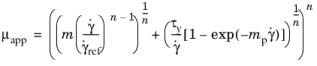
In case n equals one, it also recovers the Bingham–Papanastasiou model.
In the Ellis model, μapp is computed recursively using the following equation
(3-25)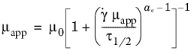
where τ1/2 is the shear stress at which
μapp = μ0/2. The exponent
ae is the shear thinning index, which is a measure of the degree of nonlinearity.
where my,0 and
τy,0 denote the consistency and yield stress of the fully broken down material, respectively,
my,0 + my,t and
τy,0 + τy,t indicate the consistency and yield stress of the fully recovered material, respectively.
(3-26)
Here, the structure field ξ obeys the following equation:
where kf and
kb denote the rebuild and breakdown coefficients, respectively.
It is also possible to add the thermal effects to the non-Newtonian constitutive models. The following options: None,
Arrhenius,
Williams–Landel–Ferry (WLF),
Exponential, and
User defined are expressed in terms of a thermal function
αT. The thermal function
αT is coupled with the non-Newtonian constitutive models by multiplying by
μ0,
μp,
m,
μDK,
my,0, and
my,0 if they are
User defined.
(3-27)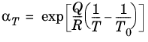
where Q denotes the activation energy,
R is the universal gas constant,
T and
T0 are the temperature and reference temperature, respectively.
(3-28)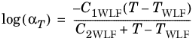
where C1WLF and
C2WLF are model constants, and
TWLF is the reference temperature.
(3-29)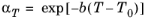
where b denotes a temperature sensitivity, and
T0 is the reference temperature.