Dielectrophoretic Force
The Dielectrophoretic Force feature adds the following contribution Fdep (SI unit: N) to the total force acting on a particle. For the case of a static nonuniform electric field,
where
•
 rp (SI unit: m) is the particle radius,
•
 ε0 = 8.854187817 × 10−12 F/m is the permittivity of vacuum,
•
 εr (dimensionless) is the relative permittivity of the surrounding fluid,
•
 εr,p (dimensionless) is the relative permittivity of the particle, and
•
 E (SI unit: V/m) is the electric field.
The electric field is assumed to change over length scales much larger than rp.
The above expression is valid for DC fields, but if the electric field is time harmonic, the dielectrophoretic force instead becomes
where and (both dimensionless) are the complex relative permittivity of the fluid and particle, respectively,
•
 σ (SI unit: S/m) is the electrical conductivity of the fluid,
•
 σp (SI unit: S/m) is the electrical conductivity of the fluid, and
•
 Erms denotes the root mean square electric field.
Dielectrophoresis of Particles with Thin Outer Shells
The Shell feature can be added to the Dielectrophoretic Force node to model the dielectrophoretic force on particles with thin outer layers. The volume inside the thin layers is assumed to have uniform conductivity and permittivity, but the properties of the shell can differ significantly from those of the rest of the particle. 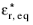When computing the dielectrophoretic force, the complex permittivity of the particle is replaced by the equivalent complex relative permittivity of a homogeneous particle comprising both the shell and the interior of the particle:
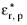
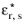
where ro and ri (SI unit: m) are the outer and inner radii of the shell, respectively; (dimensionless) is the complex relative permittivity of the particle, and (dimensionless) is the complex relative permittivity of the outer shell. If multiple shells are added, the shells are applied in the order in which they appear in the Model Builder, with the first shell being the innermost. The present treatment of spherical particles with thin shells is described in Ref. 3.