Particle Motion in a Fluid
The motion of particles in a fluid follows Newton’s second law, which states that the net force on an object is equal to the time derivative of its linear momentum in an inertial reference frame:
(5-1)
where
•
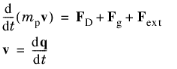
mp (SI unit: kg) is the particle mass,
•
v (SI unit: kg) is the particle velocity,
•
q (SI unit: m) is the particle position, and
•
FD, Fg, and Fext (SI unit: N) are the drag, gravity, and other forces, respectively.
In the COMSOL implementation, when the particle mass is solved for as an additional degree of freedom, such that accretion or evaporation can take place, the mass is moved outside the time derivative to prevent unphysical acceleration of the particles:
The assumption is that any mass lost by the particles continues to move with the particle velocity and does not cause the particle to decelerate.
If the virtual mass (or added mass) term is applied in addition to the drag force, then the particle mass mp on the left-hand side is replaced by the virtual particle mass mv. For more information about the virtual mass term, see the Virtual Mass Force section.
The Stokes Drag Law
In Equation 5-1, the Drag Force FD is defined as:
(5-2)
where
•
τp is the particle velocity response time (SI unit: s)
•
v is the velocity of the particle (SI unit: m/s), and
•
u is the fluid velocity (SI unit: m/s) at the particle’s position.
Strictly speaking, u is the value that the fluid velocity would have at the particle’s position if no particle were there, unless fluid-particle interactions are considered.
Many expressions for τp are available. The validity of a given drag law depends on the relative Reynolds number Rer (dimensionless) of particles in the flow,
where
•
dp (SI unit: m) is the particle diameter,
•
ρ (SI unit: kg/m3) is the density of the fluid, and
•
μ (SI unit: Pa·s) is the dynamic viscosity of the fluid.
Many expressions for the drag force, and the range of relative Reynolds numbers at which they are applicable, are given in Ref. 4.
In a creeping flow, where the relative Reynolds number is very low (Rer << 1), the Stokes drag law is applicable. This is the default behavior when adding a Drag Force node to the Particle Tracing for Fluid Flow interface. In the Stokes drag law, the velocity response time is defined as
(5-3)
where
•
μ is the fluid viscosity (SI unit: Pa·s),
•
ρp is the particle density (SI unit: kg/m3), and
•
dp is the particle diameter (SI unit: m).
By substituting Equation 5-3 into Equation 5-2, some other familiar expressions for the Stokes drag force can be obtained,
where rp (SI unit: m) is the particle radius.
Other Drag Laws
The Stokes drag law is not applicable at larger relative Reynolds numbers. Therefore, other drag laws are needed when the particles are very large, when their velocity relative to the fluid is very fast, when the fluid viscosity is low, or some combination of these factors.
To simplify the expressions for the velocity response time τp, a dimensionless drag coefficient CD is defined, such that
(5-4)
Comparing Equation 5-4 with Equation 5-3, the Stokes drag law can be stated in an alternative way, by defining the drag coefficient as
As will be shown in the following subsections, the drag coefficient in most other drag laws shows the same asymptotic behavior as the Stokes drag law for extremely small relative Reynolds numbers.
Schiller–Naumann
When Schiller-Naumann is selected from the Drag law list, the drag coefficient becomes
The Schiller–Naumann drag law is applicable over a moderate range of relative Reynolds numbers, Rer < 800.
Haider–Levenspiel
When Haider-Levenspiel is selected from the Drag law list, the drag coefficient is given by
where A, B, C, and D (all dimensionless) are empirical correlations of the particle sphericity. The sphericity is defined as the ratio of the surface area of a volume equivalent sphere to the surface area of the considered nonspherical particle
The correlation coefficients are given by
The diameter used in the Reynolds number is that of the volume equivalent sphere.
Oseen Correction
When Oseen correction is selected from the Drag law list, the drag coefficient is given by
Like Stokes drag law, the Oseen correction is applicable at low relative Reynolds numbers, typically Rer < 0.1. The Oseen correction is determined by simplifying, rather than neglecting, the inertia term in the Navier–Stokes equation, resulting in drag coefficients that are slightly greater than those based on the Stokes drag law.
Hadamard–Rybczynski
The Hadamard-Rybczynski drag law is based on an analytical solution for creeping flow past a spherical liquid drop or gas bubble. The drag coefficient is defined as
where μp (SI unit: Pa·s) is the dynamic viscosity of the droplet or gas bubble. For arbitrarily large values of μp this expression asymptotically approaches the Stokes law. The Hadamard-Rybczynski drag law is only applicable if the droplets and the surrounding fluid are extremely pure and free from surface-active contaminants. If the fluids are not sufficiently pure, the drag force on the bubble or droplet is more likely to be accurately determined by the Stokes drag law.
Standard Drag Correlations
The option Standard drag correlations defines the drag coefficient as a piecewise function of the relative Reynolds number:
Range
Correlation
 Rer ≤ 0.01
 0.01 < Rer ≤ 20
 20 < Rer ≤ 260
 260 < Rer ≤ 1500
 log CD = 1.6435 − 1.1242w + 0.1558w2
 1500 < Rer ≤ 1.2 × 104
 log CD=−2.4571+2.5558w−0.9295w2+0.1049w3
 1.2 × 104 < Rer ≤ 4.4 × 104
 log CD = −1.9181 + 0.6370w − 0.0636w2
 4.4 × 104 < Rer ≤ 3.38 × 105
 log CD = −4.3390 + 1.5809w − 0.1546w2
 3.38 × 105 < Rer ≤ 4 × 105
 CD = 29.78 − 5.3w
 4 × 105 < Rer ≤ 1 × 106
 CD = 0.1w − 0.49
1 × 106 < Rer
where w = log Rer and the base 10 logarithm has been used.
The Standard drag correlations can be used when the relative Reynolds number is expected to change by several orders of magnitude during a simulation. It is also applicable at significantly higher relative Reynolds numbers than the Schiller-Naumann drag law.
At lower relative Reynolds numbers, this correlation agrees with the Oseen correction.
The drag coefficient as a function of the relative Reynolds number is shown in Figure 5-1.
Figure 5-1: The piecewise function used to compute the drag coefficient when Standard Drag Correlations are used.
Wall Corrections
When the Include wall corrections check box is selected in the settings for the Drag Force node, the drag force is given by Ref. 5 as
(5-5)
where
•
I is the identity matrix,
•
P(n) is the projection operator onto the wall normal, n,
•
rp is the radius of the particle (SI unit: m), and
•
L is the distance from the center of the particle to the nearest wall (SI unit: m).
The first term in Equation 5-5 applies to the component of the relative particle velocity parallel to the nearest wall; the second term applies to the component of the relative velocity normal to this wall. The correction factors become more prominent as the wall distance becomes comparable to the particle radius.
Gravity Force
The Gravity Force is given by:
where
•
ρ (SI unit: kg/m3) is the density of the surrounding fluid,
•
ρp (SI unit: kg/m3) is the density of the surrounding fluid, and
•
g (SI unit: m/s2) is the gravity vector. At sea level its magnitude is approximately 9.80665 m/s2.
Because the fluid density appears in this expression, buoyancy is accounted for.