You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Friction Force feature adds the following contribution to
Ft:
where v and
u (SI unit: m/s) are the particle velocity and background fluid velocity. The collision frequency
ν (SI unit: 1/s) is either specified directly, or via a collision cross section
σ (SI unit: m
2) and background number density
Nd (SI unit: 1/m
3):
|
•
|
mp (SI unit: kg) is the particle mass,
|
|
•
|
mg (SI unit: kg) is the mass of ambient gas molecules,
|
|
•
|
q (SI unit: C) is the charge carried by particle
|
|
•
|
T (SI unit: K) is the gas temperature, and
|
|
•
|
kB = 1.380649 × 10−23 J/K is the Boltzmann constant.
|
The Mason–Schamp equation is only valid in the low electric field limit. The limit of the electric field,
E (SI unit: V/m), is measured by the ratio |
E|
/Nd, which is generally expressed in Townsend (Td) units,
1 Td =
10−21 V·m
2. A ratio of the order
10 Td or lower is usually considered as the low field. However, the range of the ratio where the Mason
–Schamp equation is valid can be different in different cases. Therefore, a proper investigation of the validity of the equation for each specific application case is required. The basic idea is that the kinetic energy of the ions should be mostly thermal, that is, the thermal energy of the charged particles should be much greater than the energy acquired from electric field between collisions.
The Collisions node uses a stochastic approach to modeling particle collisions with the atoms or molecules in a background gas. Individual collisions between the model particles and the atoms or molecules in the background gas are detected by sampling random numbers from a distribution and comparing them to the collision probability, which usually varies over time. During a collision, the velocity of the model particle changes discontinuously. Depending on the type of reaction, secondary particles may be emitted as a result of the collision.
A single Collisions node usually corresponds to a single species in the background gas. Add subnodes to the
Collisions node to specify the different reaction types that can occur between the model particles and the background gas, such as elastic collisions and charge exchange reactions.
where the νi(t) are the frequencies associated with individual reaction types between the model particle and each species in the background gas. For a time interval
Δt (SI unit: s) much smaller than the average time between collisions, the probability
PT(t) (dimensionless) that a collision takes place within a time interval of width
Δt centered at a time
t is
Let Q(t) (dimensionless) be the probability that a collision does not occur during the time interval
(0, t). Similarly,
Q(t + Δt) is the probability that a collision does not occur during the interval
(0,t + Δt).
Q(t + Δt) can be expressed the product of the probability that no collision occurs in
(0, t) (given by
Q(t)), and furthermore that no collision occurs in the interval
(t, t + Δt). The latter can be expressed as
1 − PT(t) or
1 − ν(t)Δt. Thus the relationship between
Q(t) and
Q(t + Δt) can be expressed as
Taking the limit as Δt approaches zero, the left-hand side becomes a time derivative,
Integrating and noting that Q(0) = 1 (that is, given no time, there is no possibility of a collision) yields
(4-5)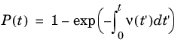
The Collisions node supports two algorithms for predicting the collision times. The algorithm is controlled by the
Collision detection list in the settings window for the
Collisions node. The two options are
At time steps taken by solver and
Null collision method, cold gas approximation.
The default option, At time steps taken by solver, can only detect and apply collisions at the discrete times used by the time dependent solver. At each one of these solution times, an uncorrelated, uniformly distributed random number
U (dimensionless) is sampled from the interval
(0, 1) for each particle. The time step is assumed to be significantly smaller than the free time between collisions,
(4-6)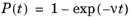
Because U is not used for any other purpose, and its actual value within the distribution has not yet been specified, we can take advantage of the equivalent probability distributions of
U and
1 − U to simplify this expression slightly:
When this option At time steps taken by solver is used, each model particle is only allowed to undergo at most one collision per time step taken by the solver. If the collision frequency is large enough so that particles are likely to undergo two or more collisions in a single time step taken by the solver, then the second and later collisions within the step are disregarded, potentially skewing the particle statistics.
In practice, the collision frequencies are usually not constant over time. In its most general form (see for example Ref. 3), the collision frequency for the
jth reaction can be expressed in terms of the corresponding collision cross section
σj (SI unit: m
2),
(4-7)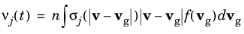
|
•
|
vg (SI unit: m/s) is the velocity of an atom or molecule in the background gas,
|
|
•
|
v (SI unit: m/s) is the particle velocity, and
|
|
•
|
n (SI unit: 1/m 3) is the number density of the gas.
|
(4-8)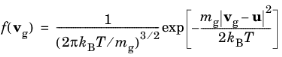
|
•
|
mg (SI unit: kg) is the mass of a gas molecule,
|
|
•
|
u is the mean or drift velocity of the background gas,
|
|
•
|
T (SI unit: K) is the gas temperature, and
|
|
•
|
kB = 1.380649 × 10−23 J/K is the Boltzmann constant.
|
Alternatively, the mass mg can be expressed in terms of the molar mass
Mg of the background species (SI unit: kg/mol),
where NA =
6.02214076 × 1023 1/mol is the Avogadro constant. Optionally, the molar mass can be assigned unique values or expressions for each reaction type.
For the option At time steps taken by solver, the following simplification is made to
Equation 4-7 to remove the integration over velocity space. First, a gas molecule velocity is sampled at random from
Equation 4-8, using a built-in
randomnormal function that creates uncorrelated Gaussian pseudorandom numbers for each velocity component. Then the velocity distribution function in
Equation 4-7 is replaced with a Dirac delta function at the sampled velocity components, yielding the simplified expression
(4-9)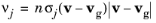
where vg now denotes the specific value of the background gas velocity sampled from the distribution.
The limiting time step size for the option At time steps taken by solver is determined from the following criteria:
The null collision method (Ref. 4) is one of a class of computational methods known as rejection methods. This approach is used by selecting
Null collision method, cold gas approximation from the
Collision detection list. The basic premise of the null collision method is to avoid inverting
Equation 4-5 for an arbitrary functional form of
ν(t) by first assigning a large, constant value
νm to the collision frequency. A number of collision times are then sampled from a distribution based on this artificially large, constant collision frequency. The sampled collision times are then either used or rejected based on an integral of the real collision frequency
ν(t) up to each trial time.
The implementation of the null collision method in the Collisions node uses a simplifying assumption known as the cold gas approximation. In applications with extremely high particle speeds, such as ions or electrons accelerating in strong electric fields, the cold gas approximation can be used to simplify the expression for collision frequency. In the cold gas approximation, the background gas velocity is set to zero, so
Equation 4-9 simplifies to
As is the case with the option At time steps taken by solver, the first step to predicting the collision times is to generate a uniformly distributed random number
U1 for each particle and compare it to the collision probability over the time interval; we use the subscript
1 here because the null collision method requires multiple uncorrelated random numbers for each model particle. Instead of the simplification made in
Equation 4-6, however, the random number is substituted directly into
Equation 4-5,
(4-10)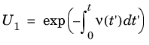
The next step is to assign a constant trial frequency νm, such that
νm > ν(t) over the interval
(0, t). Substituting the corresponding trial time
tm for
t, and
νm for
ν(t), into
Equation 4-10 and solving for
tm then yields
(4-11)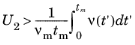
There is often no analytic expression for the integral in Equation 4-11, since the functional form that relates the collision cross section and collision frequency is not known
a priori. However, the integral can be approximated as
If the integral in Equation 4-11 were ever greater than unity, that would imply that the selected value of the trial frequency was too low and the process must be repeated, without advancing the particle in time to
tm.
The Maximum number of consecutive null collisions is available in the physics interface
Advanced Settings section. The default is
100. If any particle undergoes more null collisions than the specified value, without undergoing any real collisions, then the particle cannot collide anymore until the next time step. When this happens, a Warning is produced in the solver sequence. Consider a modest reduction in the maximum time step size if this warning appears.
A single Collisions node corresponds to a single species in the background gas. Add subnodes to the
Collisions node to specify the types of reaction that the model particles undergo with the background gas, such as elastic collisions and charge exchange reactions.
The Elastic collision force causes a particle to collide with a background gas molecule in such a way that the total energy of the system is conserved. The postcollision velocity of the particle is defined by the expression:
where g = v − vg is the relative velocity in the center of mass reference frame,
mg is the mass of the background gas atoms or molecules. The postcollision relative velocity
g′ is
g′ = |g|R where
R is a uniformly distributed random unit vector. No secondary particles are produced.
The Excitation collision force causes a particle to collide with a background gas molecule in such a way that the total energy of the system is not conserved. The postcollision velocity of the particle is defined by the expression:
where g′ = |g|R and where
where R is a uniformly distributed random unit vector, and
ΔE (SI unit: J) is the kinetic energy lost as a result of the collision. No secondary particles are produced.
The Attachment node causes the model particle to be annihilated, as in the
Disappear condition for the
Wall node. Optionally, the attached species can be released as a secondary particle that is initially at rest.
The Ionization node causes an electron to collide with a background gas molecule in such a way that the total energy of the system is not conserved. The postcollision velocity of the particle is defined by the expression:
where g′ = |g|R and where
where R is a uniformly distributed random unit vector, and
ΔE (SI unit: J) is the kinetic energy lost as a result of the collision. No secondary particles are produced.
The Resonant Charge Exchange and
Nonresonant Charge Exchange nodes are used to model collisions in which charge is exchanged between a model particle and a background gas particle. It is possible to compute the postcollision trajectories of either or both products of the charge exchange reaction. The postcollision velocity of the ionized species
v′ and neutralized species
vn′ are defined by the expressions:
and χ (SI unit: rad) is the scattering angle in the center of mass coordinate system. The vectors
g|| and
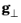
are defined by the expressions:
where ϕ (SI unit: rad) is a uniformly distributed angle between
0 and
2π. The unit vectors
e1 and
e2 are defined so that they form an orthonormal basis with the normalized precollision relative velocity
g/|g|.The postcollision relative velocity magnitude is defined by the expression:
where ΔE (SI unit: J) is the energy loss. During resonant charge exchange collisions the energy loss is
0 and
|g′| = |g|.