You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Optimization study (

) node collects all settings necessary for solving optimization problems:
The complete optimization problem can be set up directly in the Optimization study node when the objective function to be minimized or maximized is a global scalar expression, and the only control variables to be varied are already defined as model parameters. If the model requires control variables or objective functions that depend on position in the geometry, general least-squares objective contributions, or pointwise constraints, these must be set up separately using an Optimization interface. Such contributions are displayed in the
Optimization study node settings where they can be individually disabled or enabled.
When you add an Optimization study node to a study, it is always inserted as the first node, at the top of the study sequence (below any parametric sweeps). Remaining nodes in the sequence define the multiphysics problem on which the optimization process will act. If this sequence contains
Study Reference nodes and you are using a derivative-free solver, you can choose for each objective function contribution and constraint whether to compute its value for the main sequence or for the sequence pointed to by one of the study references.
The Settings window has the following sections:
Choose an optimization solver method. The Method list of available solvers contains both gradient-based and derivative-free methods.
Specify the relative Optimality tolerance. The value is applied relative to each control variable after scaling with its corresponding specified scale. The default value of this setting varies depending on the selected optimization
Method.
Choose any of the available study steps from the Study step list. Click the
Go to Source button

) to move to the
Settings window for the selected study node.
Under Solver settings you can specify the following optimization solver settings:
Specify the Maximum number of model evaluations. The default is 1000. This number limits the number of times the objective function is evaluated, which is related to the number of times the multiphysics system is simulated for different values of the optimization control parameter.
If least-squares objectives are defined, you can specify the Least-squares time/parameter method. The default is
Merge all. In that case, all least-squares defined time or parameter values are merged with the time or parameter values defined in general parameter value lists. It is possible to exclude some of the times/parameters using the
Merge within manual range option, see also
Least-Squares Data. The last option is
Use only least-squares data points. In that case, only least-squares defined time or parameter values are used and all other time or parameter values are disregarded.
For the derivative-free optimization methods — Coordinate search,
Nelder–Mead,
BOBYQA, and
COBYLA — use the
Keep solutions list to control how to store the solutions from the individual optimization solutions.
|
•
|
Select All to store all the optimizations solutions in memory.
|
|
•
|
Select Only last or Automatic (the default) to store only the last solution from the optimization job. If the there are Parametric Sweep study steps in an Optimization study, the default option ( Automatic) will save the last solution from the optimization job and all solutions from the parametric jobs.
|
Also, select the Stop if error check box to stop the optimization job at once if an error occurs.
For the gradient-based optimization methods — SNOPT,
IPOPT,
MMA, and
Levenberg–Marquardt — use the
Keep solutions list to control how to store the solutions from the individual optimization solutions:
|
•
|
Select Only last (the default) if you want to save only the last solution.
|
|
•
|
Select Last N if you want to save the last N solutions. Then specify a positive integer in the Number of solutions to save field to define N (2 by default).
|
|
•
|
Select Every Nth if you want to save every Nth solution. Specify a positive integer in the Save every Nth field to define N (10 by default to save every 10 th solution).
|
For Last N and
Every Nth, the
optSolInd parameter is created. This parameter can be used to access individual solutions with the
withsol operator (for advanced postprocessing).
You specify the objective function for the optimization problem in the table’s Expression column. Eigenvalue problems are limited to objectives expressed in terms of the eigenvalue. Otherwise, you can enter any globally available expression that evaluates to a real number. Optionally, you can add a description in the
Description column. Click the
Add Expression (

) and
Replace Expression (

) buttons to search through a list of predefined expressions.
The Evaluate for column specifies the study step for which each objective contribution will be evaluated. Available options are the last study step in the sequence plus all Study Reference nodes. When a gradient-based solver is used, the column is not active: all contributions are then evaluated for the same study step.
If there is an Optimization or
Sensitivity interface in the model, containing objective function nodes, these show up in a separate table under
Objective Function. Use the
Active column to deactivate individual contributions as needed. Contributions not supported by the currently selected solver are marked by a warning sign (

) in the first column, which disappears if you manually deactivate the objective.
Select whether to perform a Minimization or a
Maximization of the objective function. The default is to minimize the objective function.
If you have defined more than one objective function, choose how to evaluate the overall objective: Choose from Sum of objectives (the default),
Minimum of objectives, or
Maximum of objectives. Note that not all options are available together with all solvers.
Here you select which solution or solutions to use for evaluating the objective function when several solutions are present, like for Time Dependent or Eigenvalue studies. The possible choices are Auto (the default),
Use first,
Use last,
Sum of objectives,
Minimum of objectives, and
Maximum of objectives. Note that the last three options first evaluate multiple objectives according to the
Multiple objectives setting for each solution individually, and then compute the sum, minimum, or maximum of the individual results.
All options are available only with the derivative-free solvers. When using SNOPT,
IPOPT, or
Levenberg–Marquardt,
Auto is the only choice. All options are only supported with
MMA, but not when optimizing over a
Time Dependent study step.
With Auto selected, the solver chooses the evaluation method based on the innermost study. For the studies of
Eigenvalue,
Eigenfrequency, or
Linear Buckling type (all described in
COMSOL Multiphysics Reference Manual), the first solution corresponding to the smallest eigenvalue is chosen. For studies with parametric solutions (for example, studies in the
Frequency Domain), the contributions from all solutions are summed (equivalent to the
Sum of objectives option). For all other study types, the optimization solver selects the last solution, like the solution at the final time for a
Time Dependent problem, but note that least-squares objectives often have contributions for multiple values of the time parameter.
Most optimization solvers will benefit from a well-scaled objective function. You can choose between None,
Manual, or
Initial solution based scaling. The setting is available for all optimization solvers, except Levenberg–Marquardt. It will interact with the solution setting, so that the initial sum, minimum, maximum, first, or last value is chosen as the scale, if
Initial solution based scaling is used. The default value is
None. Note that the setting is not used, when the MMA optimization solver is used with least-squares objectives.
When there is a parametric sweep or a material sweep below the optimizations study step, the objective is evaluated using the Outer solutions from the sweep. The options are between the
Minimum of objectives,
Maximum of objectives, or
Sum of objectives (the default).
The first table under Control Variables and Parameters is used to select model parameters for use as control variables. Click the
Add (

) button to add one of the parameters defined in the
Settings window for
Parameters under
Global Definitions to the set of control variables.
From a list in the Parameter name column, select the parameter to redefine as a control variable. Specify an
Initial value for the control variables you add. The initial value is used as initial guess in the optimization solver and the objective function is explored around this point.
The Scale column is important. Each control variable is rescaled with its specified scale. This means, in practice, that the solvers only get to see the control variables divided by their corresponding scale, and it is on these rescaled variables that all tolerances are applied — both user-defined and internal tolerances intended to ensure the stability of the optimization methods. The default value is
1, which makes the solver work with the original, unscaled, variables.
Use the Lower bound and
Upper bound columns to add lower and upper bounds to the control variables. The Optimization solver only evaluates the objective function within these bounds. If you do not want to set bounds on a variable, leave the cell in the table empty.
Move control parameter rows up and down using the Move up (

) and
Move down (

) buttons. To remove a control parameter, select some part of that variable’s row in the table and click the
Delete button (

). You can also save the definitions of the control parameters to a text file by clicking the
Save to file button (

) and using the
Save to File dialog box that appears. To load a text file with control parameters, use the
Load from file button (

) and using the
Load from File dialog box that appears. Data must be separated by spaces or tabs.
|
|
If you have the LiveLink™ for Excel ®, you can also save and load control parameters to and from Microsoft Excel Workbook (*.xlsx) files.
|
If there is an Optimization or
Sensitivity interface in the model, containing control variable nodes, these show up in a separate table under
Control Variables and Parameters. Use the
Solve for column to deactivate individual control variables as needed. Variables not supported by the currently selected solver are marked by a warning sign (

) in the first column, which disappears if you manually choose not to include it in the solution.
The first table under Constraints lets you specify additional constraints to be imposed on the optimum solution. For eigenvalue problems the
Expression column only accepts the eigenvalue. Otherwise, you can enter any globally available expression which evaluates to a real number. Constraints can be functions of the control variables both directly and indirectly via PDE solution variables. The
Lower bound and
Upper bound columns can only contain
parameter expressions; they must not depend on control variables, PDE solution variables, or any other user-defined variables, but can include model parameters, physical constants and units. One bound column can be left blank to indicate that no upper or lower bound is required. Derivative-free optimization solvers will output orange rows in the objective probe table, if any constraints are violated.
The Evaluate for column specifies the study step for which each constraint will be evaluated. Available options are the last study step in the sequence plus all Study Reference nodes. When a gradient-based solver is used, the column is not active: all contributions are then evaluated for the same study step.
If there is an Optimization interface in the model, containing inequality constraint nodes, these also show up in a separate table under
Constraints. Use the
Active column to deactivate individual constraints as needed. Constraints not supported by the currently selected solver are marked by a warning sign (

) in the first column, which disappears if you manually choose to deactivate the constraint.
For some optimization solvers, you can select a Constraint handling method. The possible options are
Penalty and
Augmented Lagrangian. The former is the default when available and requires no further settings. Choosing the
Augmented Lagrangian method activates additional options to control its behavior and accuracy. See
Constraint Handling for Derivative-Free Methods for further details.
For derivative-free optimization solvers that support the Penalty constraint handling method (Nelder–Mead, Coordinate search) and for COBYLA you can select the
Enforce design constraints strictly check box to evaluate design constraints before the forward problem is solved and avoid running the forward problem if there are infeasible design constraints. All constraints that do not depend on the solution of the forward problem are considered to be design constraints. With the
Enforce design constraints strictly check box selected (the default), the solver evaluates all design constraints before the forward problem is run. If infeasible constraints are found, the forward problem is not run, NaN is reported as objective, and the optimization solver proceeds to the next iteration.
Select Plot and choose a
Plot group to update after each major iteration of the optimization algorithm.
Select which Probes to evaluate and plot in each iteration.
Select the Keep objective values in table check box to retain the table containing control variable and objective function values after the solver completes. Choose an existing
Output table, or select
New to create a new table. After computing the study, the
Output table setting will be changed to the table actually being used.
Select the Show individual objective values check box to include one table column for each contribution to the objective. Otherwise, only the total objective is displayed.
Select the Table graph check box to plot the objective function values displayed in the objective table. Choose an existing
Plot window, including the standard
Graphics window, or select
New window. After computing the study, the
Plot window setting will be changed to the window actually being used.
Only available for derivative-free methods. Select the Keep constraint values in table check box to retain the table containing global constraint values after the solver completes. Choose an existing
Constraint table, or select
New to create a new table. After computing the study, the
Constraint table setting will be changed to the table actually being used.
The derivative-free solvers add a new line to this table for each evaluation of the objective function. When using the Nelder–Mead,
BOBYQA, or
Coordinate search solver, the control variable and constraint values displayed on the last line correspond to the converged result of the optimization.
Specify the Confidence level (0.95 by default, meaning the 95% confidence interval). Choose an existing
Confidence interval table and
Covariance matrix table, or select
New to create new tables. If an existing table has been chosen, the data in the table will be overridden. Each row in the confidence interval table corresponds to one global control parameter in the order they are given in tables in the
Control Variables and Parameters section, assuming that the confidence interval for each parameter has been computed. When the confidence interval for some parameter cannot be computed a warning is given. The confidence intervals table is also printed out in the log. Confidence intervals for individual parameters are computed using the
t-test statistic and the linear approximation method (
Ref. 2). The confidence interval for an individual parameter
θj for a confidence level 1
− α is given by
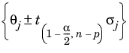
where σj is the standard deviation of the parameter
θj,
n is the number of data points, and
p is the number of parameters to identify (
Ref. 2). Here,
is the percentage point of a t-variable with
n − p degrees of freedom that leaves a probability of
α / 2 in the upper tail and 1
− α / 2 in the lower tail. The standard deviation
σj is computed using a linear approximation of the Hessian, as given in
Ref. 1. Moreover, it is assumed that the observations on the independent variable are measured without error and that the random errors in the dependent variable are normally and independently distributed. If no variance column is present, the variance of the random errors is estimated from the data. If a variance column is present, this is used as the error for computation of the (parameter) covariance matrix,
D. This can be computed using a posteriori estimator for the non-dimensional bulk variance,
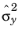
,
(5-1)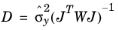 ,
,
is the sensitivity of the simulated measurements, y, to the control parameters,
p. Alternatively, the variance can be provided manually and then the computation depends on the settings for the scale. If the scale is also provided manually, the covariance matrix is computed according to
(5-2)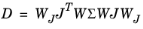 ,
,
where Σ is the (measurement) covariance matrix, and
(5-3)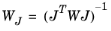 .
.
(5-4)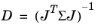
This formula requires that the inverse variance is used as weights, so the scale has to be Automatic and the variance has to be specified manually or using a data column.
Table 5-1 summarizes the relationship between the computation of the covariance matrix and the settings for the scale and variance.
If you are using a solver that supports batch evaluation of objective values, you can choose to distribute a parametric sweep by sending one parameter value to each compute node over the nodes in a cluster. To enable this functionality, first click the Show More Options button (

) and select
Batch and Cluster in the
Show More Options dialog box, then select the
Distribute parametric sweep check box. If desired, adjust the value in the
Maximum number of model evaluations in each Parametric Sweep field (default: 1). This setting in available with the following optimization solvers: Coordinate search and Nelder–Mead.
From the Optimization log list, choose
Minimal,
Normal (the default), or
Detailed to control the amount of information output from the optimization solver and the inner solvers it calls.
Select the Keep accumulated probe table check box to not remove the accumulated probe table. This setting is available with the Coordinate search, Nelder–Mead, BOBYQA, and COBYLA.