(5-7)
where dU is the change in internal energy,
dQ' is the heat flow into the system (the prime indicates an inexact differential in this case) and
dW' is the work done on the system. For a small part of a solid (sufficiently small that the stresses and strains are uniform), with an initial reference density,
ρ0, the first law can be rewritten in the following form (assuming that the differential changes occur between equilibrium states):
(5-8)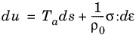
where Ta is the absolute temperature,
s is the entropy per unit mass,
σ is the elastic part of the second Piola-Kirchhoff stress (in general a rank 2 tensor),
ε is the material strain (also a tensor). In general the second Piola-Kirchhoff stress tensor,
p, must be split into elastic (
σ) and inelastic (
τ) parts such that:
The elastic part of the stress tensor, σ, does work
σ:
dε during a change in the strain. The inelastic part of the stress tensor,
τ, generates heat at a rate
τ:(
dε/dτ) when the strain is changing and is identified with internal or material damping. These internal damping mechanisms are associated with microscopic phenomena such as dislocation movement.
From Equation 5-8 it is possible to make the following identifications for
Ta and
σ:
Next the entropy balance equation must be derived. Since thermoelasticity involves irreversible processes, the assumption of equilibrium required to derive
Equation 5-8 is no longer valid. Instead an assumption of “local” equilibrium is made. It is assumed that although the system is not in equilibrium, there exists within small elements a state of local equilibrium, for which the local entropy per unit mass,
s, is the same function of the internal energy, strain, and particle number as it was in equilibrium. This assumption is commonly employed in the modeling of transport phenomena and is justified only by the validity of conclusions derived from it and by results obtained from specific microscopic models, for near-equilibrium situations. For a small volume element in the material frame
Equation 5-8 can then be written as:
(5-9)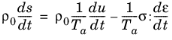
From the first law (Equation 5-7) the rate of change of internal energy is given by:
where w is the work done per unit volume and
q is the heat accumulated per unit volume. The heat accumulated can be written as the sum of the heat sources and the divergence in the material frame heat flux:
where Q represents the heat source per unit volume and
τ is the inelastic part of the stress tensor. The rate of doing work (per unit reference volume) by a linear elastic material is given by the elastic part of the second Piola–Kirchhoff stress contracted with the rate of material strain. Per unit volume the following equation is obtained:
(5-10)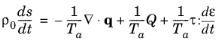
where κ is the thermal conductivity, defined in the material frame.
(5-11)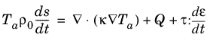
which defines a new thermodynamic potential, the Gibbs free energy per unit mass, given by:
(5-12)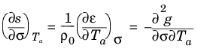
(5-13)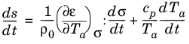
Substituting Equation 5-13 into
Equation 5-11 gives the following equation for thermoelasticity:
(5-14)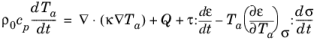
An additional heat source term is present in Equation 5-14, compared to the standard heat transfer equations in solids. This term couples the structural problem with the heat transfer problem. In turn the heat transfer equation couples back into the structural problem through the constitutive relationship.
(5-15)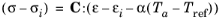
where C is the elasticity tensor,
σi is the initial stress,
εi is the initial strain, and
Tref is the reference temperature at which the strain and stresses take the initial values.
In the time domain it is convenient to linearize Equation 5-14, and this is necessary to solve problems in the frequency domain.
The independent variables in the system are Ta and
u (where
u is the displacement vector). Since the displacements drive the thermal equations it is natural to write the displacement vector as consisting of small deviations from its equilibrium value such that:
where a is a constant that is subsequently set to 1 and that is used to keep track of the order of the term in the expansion.
where a is a constant that is subsequently set to 1.
a can be used to track the order of the deviation from
T0.
Substituting these relations into Equation 5-14 and keeping terms up to the second order gives:
Note that the heat source term, Q, is assumed to be time independent (
Q = Q0). The final term in the above equation results from consideration of the Taylor expansion of the strain at constant stress, which to first order can be represented by a Taylor series of the form:
(5-16)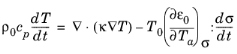
Where a=1 and the subscript has been dropped from the dependent variable
T (previously
T1) and the stress deviation
σ (previously
σ1).
Equation 5-16 is solved by the Thermoelasticity interface. Writing the equation in the frequency domain gives:
Considering the quadratic terms in Equation 5-12, there are four second-order heat source terms in the equation system:
In the frequency domain, the first three terms involve the products of small harmonic deviations with other similar terms (that is, terms that vary in time in a similar manner to cos2ω t. The trigonometric identity cos
2ω t=(1
−cos 2
ω t)/2 makes it explicit that these terms have a time-independent heating effect in addition to the heating that occurs at double the frequency of the driving signal). These second-order terms have a small effect on the time-varying solution and lead to a second harmonic term in the frequency domain. However, if the time average is nonzero, this can, over many oscillatory periods, result in a change in the background temperature. In COMSOL Multiphysics
the (nonzero) time-averaged heat sources are available as variables, so that the self-heating of the structure can be computed.
First note that the time average of the term QTED3 must be zero, since although the second-order stress term
σ2 has a nonzero time average, its time derivative cannot. The other terms in the expression for
QTED3 are all time independent. Each of the remaining terms can have a nonzero time average as these involve the multiplication of two separate first-order terms (potentially with phase differences between them). The following result for the multiplication of two general oscillatory complex numbers,
a1e
i(ωt+ϕ1) and,
a2e
i(ωt+ϕ2) are useful:
The derivation of the last term <QTED2> strongly relies on the prerequisite that the temperature dependence of the thermal expansion coefficient alpha is thermodynamically consistent. Since this prerequisite is usually not satisfied due to measurement or formulation errors, we have decided to remove the variable from the physics interface.
COMSOL Multiphysics also defines a total heat source term (
solid.Qh) of the form:
The realdot operator is used to evaluate these quantities in a manner that produces the correct terms in the Jacobian for sensitivity analyses. To compute the slow time dependence of the background temperature, the steady-state equation can be modified to allow for the time dependence of the background temperature and solved together with the frequency domain equations. In such a frequency-transient formulation, the following equations are solved: