Heat and Energy Balance
Heat Balance
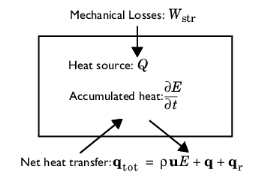
This section assumes a heat transfer model that only solves for the temperature T. In particular, for a fluid, the velocity field u and pressure field p are user defined or computed from another physics interface. In this case, the heat balance in a domain follows the identity below (chapter 11.2 in Ref. 5), derived from Equation 4-13. It expresses the idea that internal energy variations in time and net heat flux are balanced by external heat and work sources.
(4-208)
The different variables in this formula are defined in Total Heat Flux and Energy Flux. For this equality to be true, the provided dependent variables (velocity field u and pressure field p for the Navier–Stokes equations) must satisfy a mass and a momentum conservation equation. The dissipation power, Wstr, Int, contains both pressure work and viscous dissipation in fluids. The heat sources QInt include domain sources; interior boundary, edge, and point sources; and radiative source at interior boundaries.
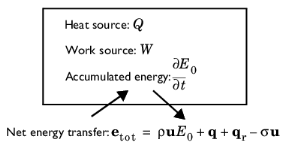
In 2D and 3D components if isolated point or edge source is not adjacent to a boundary, these are not included in QInt. In this case, these need to be computed separately.
Equation 4-208 is more visually represented by the diagram of Figure 4-46 below.
Figure 4-46: A heat balance diagram.
Several predefined variables are available in COMSOL Multiphysics to describe the heat rates involved in the system heat balance. See Global Variables for Heat and Energy Balance for their definition.
Energy Balance
When the temperature T is solved together with additional mass and momentum equations, the total energy flux also becomes a conserved quantity and the following equation holds (chapter 11.1 in Ref. 5):
(4-209)
The variables in this formula are defined in Total Heat Flux and Energy Flux. Equation 4-209 is more visually represented by the diagram of Figure 4-47 below.
Figure 4-47: An energy balance diagram.
Several predefined variables are available in COMSOL Multiphysics to describe the energy rates involved in the system energy balance. See Global Variables for Heat and Energy Balance for their definition.