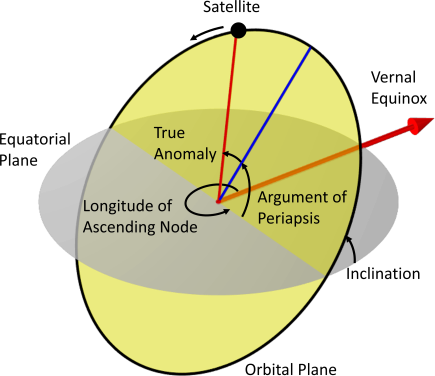
Defining the Position of the Spacecraft Over Time
To compute the orbit, the six Keplerian elements are used as in Figure 4-24: the eccentricity (e), argument of periapsis (ω), semi-major axis (a), inclination, (i) and the longitude of the ascending Node, (Ω). The beginning of the simulation can start at any point on this ellipse, as defined by the true anomaly at the simulation start time (ν0).
Figure 4-24: Definition of Keplerian elements.
It is also necessary to orient the planet at the initial time of the simulation, for the cases where the albedo or the planet radiative flux are a function of longitude and latitude, and for planet-position based orbital maneuvers. See Planet longitude at start time in the Planet Properties feature for details about the available options.
Now that the orbit is completely defined, and the position of the planet is defined, we move on to computing the spacecraft position over time.
In the orbital plane coordinate system, the coordinates of the spacecraft over time describe an ellipse. We use the solutions to Kepler’s laws to solve for the eccentric anomaly, E, and true anomaly, ν, by starting with the mean anomaly:
where the orbital period is 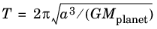and t0 is the time that it takes for the spacecraft to get from the perigee to ν0. This time is computed by integrating the swept area of the ellipse in cylindrical coordinates, centered at the planet:
where A is the total area of the orbital ellipse and the ellipse radius as a function of the true anomaly is:
Now that we can compute the mean anomaly over time, we use a series expansion to get the eccentric anomaly:
and the true anomaly:
where 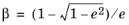and Jn are Bessel functions. In practice, only a finite number of terms, depending upon the eccentricity, in this infinite series need to be considered.
The number of terms for the series is
where [ x ] is the function that rounds to closest integer or to closest number.
Once the true anomaly over time is known, we know the position, XECS, in the ECS from the longitude of ascending node, the inclination, and the argument of periapsis:
where TECS is the transformation matrix from the orbital plane coordinate system to ECS:
To compute the times when the spacecraft goes into and out of eclipse, we introduce the concept of the solar normal plane (SNP) that is perpendicular to the Sun vector, es, and passes through the planet origin. The spacecraft position can be projected onto this plane:
When || XSNP || < Rplanet and if the spacecraft is in front of the solar normal plane es ⋅ XECS > 0, the spacecraft is in eclipse.