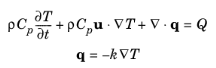Solid
This node uses this version of the heat equation to model heat transfer in solids:
(6-15)
with the following material properties, fields, and sources:
•
ρ (SI unit: kg/m3) is the solid density.
•
Cp (SI unit: J/(kg·K)) is the solid heat capacity at constant pressure.
•
k (SI unit: W/(m·K)) is the solid thermal conductivity (a scalar or a tensor if the thermal conductivity is anisotropic).
•
u (SI unit: m/s) is the velocity field defined by the Moving Mesh node when parts of the model are moving in the material frame.
•
Q (SI unit: W/m3) is the heat source (or sink). Add one or more heat sources as separate physics features. See Heat Source node and Thermoelastic Damping subnode for example.
For a steady-state problem the temperature does not change with time and the first term disappears.
Model Input
This section contains fields and values that are inputs for expressions defining material properties. If such user-defined property groups are added, the model inputs appear here.
Volume Reference Temperature
This section is available when a temperature-dependent density defined in a material is used. On the material frame, the density is evaluated in relation to a reference temperature in order to ensure conservation of the mass in the presence of temperature variations. By default the Common model input is used. This corresponds to the variable minput.Tempref, which is set to 293.15 K by default. To edit it, click the Go to Source button (), and in the Default Model Inputs node under Global Definitions, set a value for the Volume reference temperature in the Expression for remaining selection section.
The other options are User defined and all temperature variables from the physics interfaces included in the model.
This model input does not override the Reference temperature Tref set in the Physical Model section of the physics interface, which is used to evaluate the reference enthalpy, and a reference density for incompressible nonisothermal flows.
Temperature
This section is available when material properties are temperature-dependent. By default, the temperature of the parent interface is used and the section is not editable. To edit the Temperature field, click Make All Model Inputs Editable (). The available options are User defined (default), Common model input (the minput.T variable, set to 293.15 K by default) and all temperature variables from the physics interfaces included in the model. To edit the minput.T variable, click the Go to Source button (), and in the Default Model Inputs node under Global Definitions, set a value for the Temperature in the Expression for remaining selection section.
Heat Conduction, Solid
The thermal conductivity k describes the relationship between the heat flux vector q and the temperature gradient ∇T in q = −k∇T, which is Fourier’s law of heat conduction. Enter this quantity as power per length and temperature.
The default Thermal conductivity k is taken From material. For User defined select Isotropic, Diagonal, Symmetric, or Full based on the characteristics of the thermal conductivity, and enter another value or expression. For Isotropic enter a scalar which will be used to define a diagonal tensor. For the other options, enter values or expressions into the editable fields of the tensor.
The components of the thermal conductivity k when given on tensor form (kxx, kyy, and so on, representing an anisotropic thermal conductivity) are available as ht.kxx, ht.kyy, and so on (using the default name ht). The single scalar mean effective thermal conductivity ht.kmean is the mean value of the diagonal elements kxx, kyy, and kzz.
When the material and spatial frames differ (due to the presence in the model of a Moving Mesh node, or a Solid Mechanics interface for example), you can select on which frame the thermal conductivity is specified.
By default the Deformation model for thermal conductivity is set to Standard. With this option, the thermal conductivity is supposed to be given on the material frame. If the material frame does not coincide with the spatial frame, a conversion is applied to get the variables ht.kxx, ht.kyy, and so on. This option is often suitable for moderate elastic strains.
By selecting the Large strain option, the thermal conductivity is supposed to be given on the spatial frame. In case of isotropic materials, the thermal conductivity variables ht.kxx, ht.kyy, and so on, are directly equal to the values you have set. In case of anisotropic materials, the rotation of the material is also taken into account following
where R is the rotation matrix between the material and the spatial frames.
Fourier’s law assumes that the thermal conductivity tensor is symmetric. A nonsymmetric tensor can lead to unphysical results.
Thermodynamics, Solid
This section defines the thermodynamics properties of the solid.
The heat capacity at constant pressure describes the amount of heat energy required to produce a unit temperature change in a unit mass.
The Density ρ and Heat capacity at constant pressure Cp should be specified.
In addition, the thermal diffusivity α, defined as k ⁄(ρ Cp) (SI unit: m2/s), is also a predefined quantity. The thermal diffusivity can be interpreted as a measure of thermal inertia (heat propagates slowly where the thermal diffusivity is low, for example). The components of the thermal diffusivity α, when given on tensor form (αxx, αyy, and so on, representing an anisotropic thermal diffusivity) are available as ht.alphaTdxx, ht.alphaTdyy, and so on (using the default physics name ht). The single scalar mean thermal diffusivity ht.alphaTdMean is the mean value of the diagonal elements αxx, αyy, and αzz. The denominator ρ Cp is the effective volumetric heat capacity which is also available as a predefined quantity, ht.C_eff.
•
Theory for Heat Transfer in Porous Media
•
Theory for Heat Transfer in Solids
The Thermoelastic Damping subnode is available from the context menu (right-click the parent node) or from the Physics toolbar, Attributes menu.
Heat Generation in a Disc Brake: Application Library path Heat_Transfer_Module/Thermal_Contact_and_Friction/brake_disc
For a detailed overview of the functionality available in each product, visit https://www.comsol.com/products/specifications/
Location in User Interface
Context Menus
Heat Transfer in Solids and Fluids>Solid
Heat Transfer in Solids>Solid
Heat Transfer in Fluids>Solid
Heat Transfer in Porous Media>Solid
Heat Transfer in Building Materials>Solid
Bioheat Transfer>Solid
Ribbon
Physics tab with interface as Heat Transfer in Solids and Fluids, Heat Transfer in Solids, Heat Transfer in Fluids, Heat Transfer in Porous Media, Heat Transfer in Building Materials, or Bioheat Transfer selected:
Domains>interface>Solid