Participating Medium (Radiation in Participating Media Interface)
This node should be used when radiation occurs in a medium not completely transparent, in which the radiation rays interact with the medium. It calculates the heating due to the propagation of the rays, and takes into account the absorbed, the emitted, and the scattered radiation, depending on the Radiation discretization method selected in the Participating Media Settings section of the interface.
It calculates the radiative heat source term Q (SI unit: W/m3), defined by:
where
•
κ is the absorption coefficient (SI unit: m–1).
•
G is the incident radiation (SI unit: W/m2).
•
Ib(T) is the blackbody radiative intensity (SI unit: W/(m2·sr)), defined as
•
  nr is the refractive index (dimensionless).
•
 σ is the Stefan-Boltzmann constant (SI unit: W/(m2·K4)).
•
 T is the temperature (SI unit: K)
G is defined by
where
•
 I(Ω) is the radiative intensity (SI unit: W/(m2·sr)) at a given position following the Ω direction, that satisfies the radiative transfer equation
•
 β = κ + σs is the extinction coefficient (SI unit: 1/m).
•
 σs is the scattering coefficient (SI unit: 1/m).
•
 ϕ(Ω', Ω) is the scattering phase function (dimensionless)
If the Radiation discretization method is Discrete ordinates method, G is defined by
(6-10)
and, in a cartesian coordinates system
(6-11)
where
•
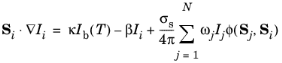
 Si is the ith discrete ordinate.
•
 Ii is the ith component of the radiative intensity.
•
 ωj is the ith quadrature weight.
If the Radiation discretization method is P1 approximation, G is the solution of the following equation
(6-12)
where DP1 is the P1 diffusion coefficient.
When Wavelength dependence of radiative properties is Solar and ambient or Multiple spectral bands in the Participating Media Settings section of the interface, Equation 6-10 and Equation 6-11 are solved for each spectral band k: Ii,k is the ith component of the radiative intensity for spectral band k, and Gk is the incident radiation for spectral band k.
The characteristics of the two available radiation discretization methods are summarized in the following table.
Table 6-3: Discretization methods for Participating Medium (RPM interface).
Option
DOM
P1
Optical thickness validity
All
τ>>1
Absorption modeling
Yes
Yes
Emission modeling
Yes
Yes
Scattering modeling
Linear
Polynomial (in 2D and 3D)
Linear
Computational cost
High: up to 80 additional degrees of freedom (Ii)
Medium: 1 additional degree of freedom (G)
If radiative emission may be neglected, the Absorbing-Scattering Medium (Radiation in Absorbing-Scattering Media Interface) node may be used instead. The table below describes the different effects accounted for by the interfaces found under the Heat Transfer>Radiation branch ().
Table 6-4: Radiation Effects calculated by the Radiation Interfaces.
Radiation Effect
RPM
RASM
RBAM
Absorption
Yes
Yes
Yes
Scattering
Yes
Yes
No
Emission
Yes
No
No
Model Input
This section contains fields and values that are inputs for expressions defining material properties. If such user-defined property groups are added, the model inputs appear here.
Temperature
This section is available when temperature-dependent material properties are used. The default Temperature is User defined. When additional physics interfaces are added to the model, the temperature variables defined by these physics interfaces can also be selected from the list. The Common model input option corresponds to the minput.T variable, set to 293.15 K by default) and all temperature variables from the physics interfaces included in the model. To edit the minput.T variable, click the Go to Source button (), and in the Default Model Inputs node under Global Definitions, set a value for the Temperature in the Expression for remaining selection section.
Fractional Emissive Power
This section is available when the Wavelength dependence of radiative properties is defined as Solar and ambient or Multiple spectral bands for the physics interface (see Participating Media Settings).
When the Fractional emissive power is Blackbody/Graybody, the fractional emissive power is automatically calculated for each spectral band as a function of the band endpoints and temperature.
When the Fractional emissive power is User defined on each band, define the Fractional emissive power, FEPk for each spectral band. All fractional emissive powers are expected to be in [0,1] and their sum is expected to be equal to 1.
Absorption
The Absorption coefficient κ should be specified. It defines the amount of radiation, κI(Ω), that is absorbed by the medium.
The Absorption coefficient κ (SI unit: 1/m) uses values From material by default.
For User defined, set a value or expression. You can define a temperature-dependent absorption coefficient using the variable rpm.T.
If Wavelength dependence of radiative properties is Solar and ambient or Multiple spectral bands, the wavelength may be accessed through the rpm.lambda variable. Any expression set for the absorption coefficient is then averaged on each spectral band to obtain a piecewise constant absorption coefficient. If the average value of the absorption coefficient on each band is known, you may use instead the User defined for each band option to avoid the evaluation of the average.
When Absorption coefficient is set to User defined for each band, enter a value for the Absorption coefficient for each spectral band in the table displayed underneath. Within a spectral band, each value is assumed to be independent of wavelength.
Scattering
This section defines the scattering property of the participating medium. The Scattering coefficient σs should be specified.
The Scattering coefficient σs (SI unit: 1/m) uses values From material by default.
For User defined, set a value or expression. You can define a temperature-dependent scattering coefficient using the variable rpm.T.
If Wavelength dependence of radiative properties is Solar and ambient or Multiple spectral bands, the wavelength may be accessed through the rpm.lambda variable. Any expression set for the scattering coefficient is then averaged on each spectral band to obtain a piecewise constant scattering coefficient. If the average value of the scattering coefficient on each band is known, you may use instead the User defined for each band option to avoid the evaluation of the average.
When Scattering coefficient is set to User defined for each band, enter a value for the Scattering coefficient for each spectral band in the table displayed underneath. Within a spectral band, each value is assumed to be independent of wavelength.
Choose in addition the Scattering type: Isotropic, Linear anisotropic, Polynomial anisotropic (only with Discrete ordinates method), or Henyey-Greenstein (only with Discrete ordinates method). If the Radiation discretization method is Discrete ordinates method, only Isotropic is available for 2D axisymmetric components.
This setting provides options to approximate the scattering phase function ϕ using the cosine of the scattering angle, μ0:
•
Isotropic (default) corresponds to the scattering phase function ϕ(μ0) = 1.
•
For Linear anisotropic it defines the scattering phase function as ϕ(μ0) = 1 + a1μ0. Enter the Legendre coefficient a1.
•
For Polynomial anisotropic it defines the scattering phase function as
Enter each Legendre coefficient a1, …, a12 as required.
•
For Henyey-Greenstein it defines the scattering phase function as
where −1 < η < 1 is the anisotropy parameter and K is defined as follows to produce a normalized phase function:
For Linear anisotropic and Polynomial anisotropic, select the Normalize phase function check box to define a phase function such as
The normalization is automatically applied for the Henyey-Greenstein option.
For Linear anisotropic, Polynomial anisotropic, and Henyey-Greenstein, select the Wavelength-dependent scattering type check box to average each Legendre coefficient a1, …, a12 or the Anisotropy parameter μ to obtain piecewise constant coefficients on each spectral band.
•
Theory for Radiation in Participating Media
•
Discrete Ordinates Method (DOM)
•
P1 Approximation Theory
Radiative Heat Transfer in a Utility Boiler: Application Library path Heat_Transfer_Module/Thermal_Radiation/boiler
Radiative Cooling of a Glass Plate: Application Library path Heat_Transfer_Module/Thermal_Radiation/glass_plate
Radiative Heat Transfer in Finite Cylindrical Media: Application Library path Heat_Transfer_Module/Verification_Examples/cylinder_participating_media
Radiative Heat Transfer in Finite Cylindrical Media — P1 Method: Application Library path Heat_Transfer_Module/Verification_Examples/cylinder_participating_media_p1
Location in User Interface
Context Menus
 Radiation in Participating Media>Participating Medium
Ribbon
Physics tab with Radiation in Participating Media selected:
Domains>Radiation in Participating Media>Participating Medium