Domain Decomposition (Schwarz)

The node (

) is an attribute node that can be used together with the Iterative and Coarse Solver nodes. Use it to set up an additive, multiplicative, hybrid, or symmetric Schwarz overlapping domain decomposition solver. Domain decomposition divides the modeling domain into subdomains where the equations in the subdomains are easier to solve. The total solution is then obtained by iterating between the computed solutions for each subdomain using the currently known solutions from the other subdomains as boundary conditions. The domain decomposition (Schwarz) solver is efficient for distributed memory systems (cluster computing) and as a more memory-efficient alternative to a direct solver for large problems.

Default Coarse Solver and Domain Solver nodes are also added. The domain solver can be any of the direct and iterative solvers, and also a geometric multigrid solver. When you use a multigrid solver as the domain solver for domain decomposition, each domain solves an independent linear problem using a multigrid solver. Each linear problem is created from the underlying multigrid solver’s mesh case hierarchy. The domain problems can then be solved independently.

•

. The default is 100,000 DOFs. The solver tries to not create subdomains larger than this and increases the number of subdomains to fulfill the target. The lowest value accepted is 1000.

•

. The default is 1. This option is only relevant in cluster computations. Each subdomain is then handled by the selected number of compute nodes.

•

. The default is 1 mesh element. Each subdomain in the initial (nonoverlapping) partition is extended via the connectivity of the stiffness matrix in a recursive algorithm or by the connectivity of the mesh (see ); this setting controls the number of additional mesh elements — added to the necessary single mesh element — in the overlap between adjacent subdomains.

•

: (the default), , or . The automatic setting chooses the overlap method based on the matrix format used. The matrix-based overlap method considers the matrix connectivity whereas the mesh-based overlap method considers neighboring mesh elements. Select if the matrix-based overlap generates too large overlapping subdomains.

•

: (default), , , or . These options affect the definition of the restriction operators and have benefits in terms of less communication on cluster and less iteration numbers for Additive Schwarz methods.

•

: (the default), , or . The option creates a subdomain distribution by means of the element and vertex lists taken from the mesh. This option typically gives a low number of colors and gives balanced subdomains (equal number of DOFs, small subdomain interfaces, and a smaller overlap if extended). To avoid slim domains, you can also use a preordering algorithm based on a . The following plots show a 2D subdomain configuration without element preordering (left) and with an element reordering based on a space-filling curve (right):

•

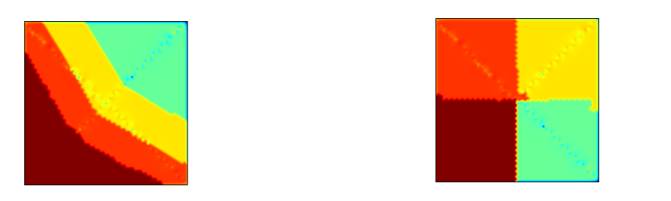Choose an option from the list if required: (default), , or . The option is a computationally expensive option because the subdomain problems are factorized for each iteration and then cleared from memory. If you use the option, the recompute and clear mechanism is activated if there is an out-memory-error during the domain decomposition setup phase. The setup is then repeated with recompute and clear activated. A warning is given in this case.

•

If or is selected as the , the check box is selected by default to use a coloring technique that leads to more efficient computations for the multiplicative and symmetric methods because they require the global residual to be updated after each subdomain. The coloring technique gives each subdomain a color such that subdomains with the same color are disjoint and can be computed in parallel before the residual is updated. Click to clear the check box as needed.

•

Select the check box to automatically choose the matrix free format, which can save memory. Then select a boundary condition from the list: , (the default), , or (see The Domain Decomposition Solvers). The ’s settings are described in Absorbing Boundary Condition below. To improve the convergence rate for large Helmholtz-type problems, select the check box. See Shifted Laplace Contribution (CSL) below.

•

In the list, include the geometries (components) in the model that you want to partition using domain decomposition. By default, this list includes all geometries in the model. Use the (

), (

), and (

) buttons to configure the lists of geometries.

•

The check box is selected by default to include extra dimension in the domain decomposition partitioning in models that include extra dimensions. Clear the check box to exclude any extra dimensions from the partitioning.

•

Select the check box to visualize the domains in the domain decomposition using a surface plot, for example. The plot then shows the numbering of the domains instead of the physics solution. A node appears in the solver configuration under the node to inform you that the solution can only be used to visualize domains in the domain decomposition. You will then have to re-solve the model to postprocess the physics in the model.

•

: This option uses the Nicolaides coarse space as a way of constructing a coarse space for Schwarz domain decomposition. This option has no additional settings because it does not need any additional information, such as a coarser mesh, except the local system matrices from the local domains. It is useful when computing a coarse grid when , , and are not feasible. For instance, if they require too much memory or are too expensive to compute. Using improves the convergence rate compared to the option.

•

. The default. Generates first a coarse level by lowering the order (by one) of any of the used shape functions. If there are no shape functions that can be lowered, the mesh is coarsened.

•

. Generates first a coarse level by lowering the order (by one) of all the used shape functions. If this is not possible, the mesh is coarsened.

•

. Generates a coarse level by lowering the order (by one) of all the used shape functions. If this is not possible, the mesh is refined a number of times. The mesh solved for can, with this method, be a finer one than the one selected under the study node.

•

. Generates a coarse level by lowering the order (by one) of any of the used shape functions. If there are no shape functions that can be lowered, the mesh is refined. The mesh solved for can, with this method, be a finer one than the one selected under the Study node.

•

. Use this setting to select a coarse multigrid level from the existing ones. You then specify the coarse multigrid level to use in the list. Use the (

), (

), and (

) buttons to configure the list of multigrid levels. Use the check box to assemble the discrete differential operators on the coarse multigrid level (selected by default).

•

In the list, select the geometries to apply the coarse multigrid level to. Use the (

), (

), and (

) buttons to configure the list of geometries.

•

The check box is selected by default to assemble the discrete differential operators. Otherwise, these operators are formed using the restriction and prolongation operators. Click to clear the check box as needed.

•

Enter a to select the degree of coarsening to apply to the meshes when using mesh coarsening as the multigrid hierarchy generation method. The higher this number, the more aggressive the mesh coarsening is. The default is 2.

When , , or are selected from the list, select a to refine the multigrid levels when using mesh refinement as the multigrid hierarchy generation method. The options are:

•

. The default method. Elements are subdivided such that the longest side in each element is always split. This yields not so many new elements, while also preserving mesh quality.

•

To enter a , first select the associated check box. If the check box is cleared (the default), the value is taken from the field. The default is 5000. Coarse levels are added until the number of DOFs at the coarsest level is less than the max DOFs at coarsest level or until it has reached the number of multigrid levels.

•

Enter a value or use the slider to set the . Higher quality means faster convergence at the expense of a more time-consuming setup phase. For instance, if the linear solver does not converge or if it uses too many iterations, try a higher value to increase the accuracy in each iteration, meaning fewer iterations. If the algebraic multigrid algorithm runs into memory problems, try a lower value to use less memory. The range goes from 1 to 10, where 10 gives the best quality. The default is 3.

•

The check box is selected by default. This setting provides the combination of GMG with lower order until order 1 is reached and then uses AMG to generate the coarser levels. The check box, which is selected by default, then corresponds to the GMG option top assemble on all level. Using this setting is equivalent to using GMG with AMG as a coarse grid solver.

•

The aggregation algorithm is based on a connection criterion, which you specify as a coefficient in the field. A node j is connected to another node i, if

, where ε is the strength of connection coefficient, and Aij is the submatrix of the stiffness matrix defined by the degrees of freedoms on node i and j, respectively. Loosely speaking, the strength of connection value determines how strongly the aggregation should follow the direction of anisotropy in the problem. The default value is 0.01.

•

From the list, choose (the default) or . For linear elasticity problems, always select because it enhances the convergence properties significantly.

•

Select the check box to do the construction on each component, which can be a good choice for not strongly coupled physics. This check box is only available when the list is set to .

•

Choose how to control the prolongator smoothing using the list, which is active when the check box (selected by default) is selected. The option postpones the smoothing for sdim-1 levels, where sdim is the space dimension of the problem. If you choose , enter the level to start smoothing at in the field.

where ω is the Jacobi damping factor, AF is the filtered stiffness matrix, and D is the diagonal of AF. Specify ω in the field. The default value is 2/3.

•

By default, the check box is selected. Filtering means that entries in the stiffness matrix have been dropped if they correspond to degrees of freedoms on a node that has no strong connections. Loosely speaking, filtering highlights anisotropy in the problem and results in a sparser coarse level problem.

•

The check box is selected by default. This setting provides the combination of GMG with lower order until order 1 is reached and then uses SAAMG to generate the coarser levels. The check box, which is selected by default, then corresponds to the GMG option top assemble on all level. Using this setting is equivalent to using GMG with SAAMG as a coarse grid solver. In order to solve a coarse grid correction problem, the prolongation matrices are multiplied into a single matrix that maps from the fine level to the coarse level.

Select the check box to add the term to the coarse grid level. The options are the same for the fine grid level as described in the section above. The created feature is a .

: The code internally creates an node for the selected physics. Specify a zero-order coefficient as a scalar value in the field (default: 0.75). You can add a second-order term by selecting the check box and specifying a second-order coefficient (default: 0.005). These coefficients correspond to α and β, respectively, in the following equation for an absorbing boundary condition:

The option is only supported for the Helmholtz equation. Select the check box in order to keep the feature in the Physics node.

: Specify the complete weak-form expression in the field. This expression can be applied to any Physics available in the list above. Select the check box to keep the feature in the Physics node.

: the is taken from the Physics node. Only use this option if a weak contribution feature was previously added by selecting the check box together with the or options as described above.

: The code internally creates a feature for the selected physics. Specify a relaxation factor, which is a scalar value (default: 1). The shift coefficient multiplies the expression for the shifted Laplace contribution. You can think of it as the β coefficient in the Complex Shifted Laplacian for Large Helmholtz Problems section. It might be the case that you need more or less damping than what the original equation provides; you can then choose another value for this factor. The option is only supported for Helmholtz-type equations. In that case, the meaning of the shift coefficient is the factor α in the term −i α kru, where r is 1. Select the check box in order to keep the feature in the Physics node.

: Specify the complete weak-form expression in the field. This expression can be applied to any Physics available in the list above. The added weak term does not modify the solution of the original problem. It is only used on the multigrid levels to help with convergence. Select the check box to keep the feature in the Physics node.

: the feature is taken from the Physics node. Only use this option if a weak contribution feature was previously added by selecting the check box together with the or options as described above.

Also see the section “Complex Shifted Laplacian for Very Large Frequency Domain Models” in the Acoustics Module User’s Guide for an example of how to set up the shifted Laplace contribution for a pressure acoustics model.

If you have selected the check box, the settings there are the same as for the shifted Laplace contribution above but used on the coarse level.

User the settings in the section to set up a hybrid preconditioner where the direct preconditioner is active for some dependent variables. See Hybrid Preconditioners for more information.