For the Solution termination criterion: When termination of the
Segregated solver is based on the estimated error, it terminates if, for all the groups
j, the error estimate is smaller than the corresponding tolerance,
The number tolj is the relative tolerance for the corresponding group. For each degree of freedom (DOF), the field variable solved for is
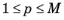
and
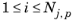
is the index of that DOF. The largest damped Newton error is then estimated by:
Here l is taken for all iterations in all substeps solving for the group
j,
αl,j is the damping factor,
ΔU l, j, k,p is the Newton increment vector, and
Nj,p is the number of DOFs in the field
p. The weight factor
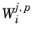
is described below. Moreover,
is the relative increment over one complete iteration k. In this expression,
Uj,k,p is the segregated solution vector for the group
j, and
where Si is a scale factor that the solver determines from the settings in the
Scaling section of the
Settings window for the
Dependent Variables node, where the following choices are available in the
Method list:
For the Residual termination criterion, the segregated solver terminates when the following convergence criterion is satisfied: For all the groups
j, the error estimate is smaller than the corresponding tolerance,
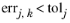
, where
where F is the current residual, and
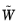
are the weights determined by the first and, if applicable, the second residual. The iterations can also terminate if the relative solution-based error is in the range of a hundred machine epsilon.
Pseudo time stepping is available in a stationary segregated approach as well; see Pseudo Time Stepping for a description of the CFL control. For the segregated solver, the error estimate
en in
Equation 20-1 is the arithmetic average of the errors in the different segregated groups.