COMSOL 6.2 - Entering Quality Settings for Plot Settings Windows

Many plots have a section where you can specify all or some of the plot resolution, to enforce continuity, smoothing, the use of accurate derivative recovery, and the use of derivatives. The steps for this section vary slightly based on the plot but are basically as follows.

Under , select a plot : , , , (the default), , , or . A higher resolution means that elements are split into smaller patches during rendering. The , , , use heuristics to determine a suitable resolution. For , enter a positive integer (default: 1) in the field. A higher value means higher resolution. The refinements is done by subdividing the element edges. See the following figure, which shows the refinement levels 1, 2, and 3:

	Custom refinement applies to the base dataset. The number of elements in the model can therefore increase radically if the plot uses, for example, a revolve dataset because the refinement is applied to the solution dataset.

(the default): to smooth the quantity within domains shared by the same material but not across material boundaries. Here, material is interpreted in a wider sense than just a physical material. Some physics interfaces implement material groups, which are sets of domains that are considered as being suitable for internal smoothing.

: to smooth the quantity inside the geometry, but no smoothing takes place across borders between domains with different settings.

: to use an expression to indicate where smoothing should occur. Enter an expression in the field such that smoothing occurs where the expression is continuous. The default expression is dom, the domain variable, which is equivalent to the smoothing. You can also — in a surface plot, for example — use material.domain, which is an indicator variable for domains that share the same material (see Material Group Indicator Variables) and is equivalent to the setting.

For all settings except , you can specify a smoothing threshold by choosing from the list and specify a value in the field. The default is , for no smoothing threshold.

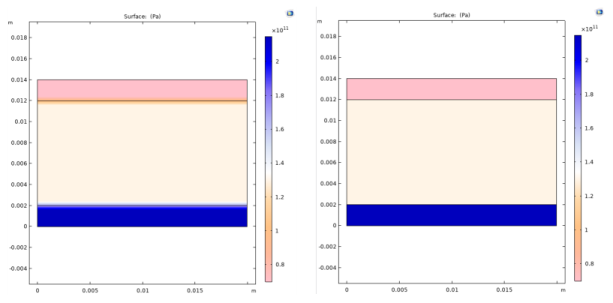
The default, , is to smooth the quantity except across borders between domains with different materials, where there is often a sharp transition from one material to another or between different types of physics. See the screenshots below that shows a material discontinuity where smoothing everywhere blurs the border (left) whereas smoothing inside material domains (right) keeps the material discontinuity intact. In these plots, no refinement is used to show the smoothing effect more clearly.

Under , the default is because the accurate derivative recovery takes processing time. This recovery is a polynomial-preserving recovery that recovers fields with derivatives such as stresses or fluxes with a higher theoretical convergence than smoothing (see Polynomial-Preserving Derivative Recovery below).

	The Recover option only affects variables that are defined on domains.

The check box is selected by default, when available. Clear it if you do not want to use space derivatives for a smoother plot, but doing so usually improves the plot quality.

Plotting and evaluating stresses or fluxes boils down to evaluating space derivatives of the dependent variables. By default, computing a derivative like ux or uxx (first and second derivatives of u with respect to x) is done by evaluating the derivative of the shape functions used in the finite element approximation. These values have poorer accuracy than the solution u itself. For example, uxx is identically 0 if u is defined using linear elements. COMSOL Multiphysics evaluates the derivatives (and u itself) using a polynomial-preserving recovery technique by Z. Zhang (see Ref. 1). The recovery is only applied on variables that are discretized using Lagrange shape functions.

The polynomial-preserving recovery is a variant of the superconvergent patch recovery by Zienkiewicz and Zhu that forms a higher-order approximation of the solution on a patch of mesh elements around each mesh vertex. For regular meshes, the convergence rate of the recovered gradient is O(hp+1) — the same as for the solution itself. Near boundaries, the accuracy is not as good, and it might even be worse than without recovery. Results evaluation is about 2–5 times slower when using polynomial-preserving derivative recovery.

By default, the accurate derivative recovery smooths the derivatives within each group of domains with equal settings. Thus, there is no smoothing across material discontinuities. You find the setting for accurate derivative recovery in the plot node’s windows’ section. Due to performance reasons, the default value for list is (that is, no accurate derivative recovery). Select to smooth the derivatives within each domain group (that is, groups of domains with equal settings). Select to smooth the derivatives across the entire geometry.