The Edit mixing rule dialog box is used to control the mixing rules in the material contents table of a Multiphase Material or Effective Material.

To open the Edit mixing rule dialog:

If there are several material properties in the table, you can step through the table without closing the dialog using the Previous Row (Discard Changes) (), Previous Row (Store Changes) (), Next Row (Discard Changes) (), and Next Row (Store Changes) () toolbar buttons. The current row of the is identified by the Property Group and Parameter fields.

where n is the number of phases, Vf,i is the volume fraction of phase i, X is the effective material property, and Xi is the material property of phase i.

where wi is the mass fraction of phase i,

Here, ρ is the effective density and ρi is the density of phase i.

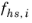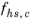
where is the fraction used for phase i, is the fraction corresponding to the constrained phase, and lmix is a user-defined mixing parameter (default: 0.8) defining the size of the transition zone between phases for the smooth Heaviside function H.

The effective structural material properties of composites depend on the material properties of the constituents and their geometric arrangements. These can be approximated either analytically or numerically. The numerical approach is applicable to a broader range of geometrical configurations, but is more complicated to use. The Effective Material includes a list of analytical approaches that are simple and handy, aimed at cases where an orthotropic fiber acts as reinforcement of an isotropic matrix. These methods are taken from Ref. 1, Ref. 2, and Ref. 3.

In this section, the properties of the fiber reinforcements are denoted by subscript f, while properties of the matrix are denoted by m. The mixing rules for composites are only available to a specific set of material properties. These rules should be used together with a Volume Averaged mixing rule for density.

The Halpin–Tsai model includes empirical factors ζ for the components of the elastic modulus and are a measure of the reinforcement that depends on fiber geometry. Some typical values for the orthotropic Young’s modulus are depicted in the table value. The value of ζ for the components of G is typically 1.

In the table above, l11 is the fiber length in the 11 direction, w22 is the fiber width in the 22 direction, and t33 is the fiber thickness in the 33 direction.

The Halpin–Tsai–Nielsen model extends the Halpin–Tsai model by accounting for the maximum packing fraction of the reinforcement, (default 0.82). Typical values of the maximum packing factor are listed in Table 9-7.

and the effective properties are given by Table 9-8.

The bulk modulus of fiber, Kf, and matrix, Km, under longitudinal strain are

The bulk modulus of the composite K under longitudinal strain is

In this model, the effective shear modulus of the composite G23 is approximated from the quadratic equation

The effective material properties are then given by Table 9-9.

The effective dynamic viscosity μ in suspensions may be modeled using the Krieger-type model as

When Krieger type viscosity is selected, enter a value or expression for the Maximum packing concentration 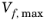(dimensionless). The default is 0.62.