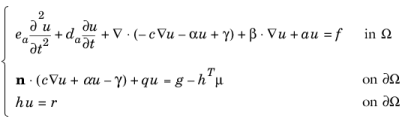An algebraic multigrid solver or preconditioner that performs one or more cycles of a multigrid method using a coarsening of the discretization based on the coefficient matrix. Compare to geometric multigrid (GMG).

An API provides a set of documented functions and methods for interacting with a software product.

A formulation where an Eulerian equation is transformed into an equation written with respect to a mesh, which can be moving in relation to both the Eulerian frame and the Lagrangian frame. The COMSOL Multiphysics solvers have built-in support for the necessary transformation of derivatives.

A 2D, 6-node triangular finite element with a 5th-order basis function providing continuous derivatives between elements.

Taking the local element stiffnesses, masses, loads, and constraints to form the stiffness matrix, mass matrix, load vector, constraint matrix, and constraint residual vector.

An algorithm that maps data associated with a geometric model to the new geometric entities when the geometric model is modified.

A multistep formula based on numerical differentiation for solutions to ordinary differential equations. A BDF method of order n computes the solution using an nth-grade polynomial in terms of backward differences.

A function φi in the finite element space such that the ith degree of freedom is 1, while all other degrees of freedom are 0. For the Lagrange finite element space, φi is a linear or higher-order polynomial on each mesh element with value 1 in node i and 0 in all other nodes.

See Galerkin boundary element method.

See Bézier basis.

A set of polynomial functions that occur in the definition of a Bézier curve. These polynomial functions are often called Bernstein polynomials.

A rational Bézier curve is a parameterized curve formed as the quotient of two polynomials expressed in the Bézier basis. It is a vector-valued function of one variable. The coefficients of a rational Bézier curve are geometrically interpreted as control points and control weights. A nonrational Bézier curve is a rational Bézier curve with all weights equal, thereby making the denominator polynomial equal to a constant. A nonrational Bézier curve is also called an integer Bézier curve.

A Bézier patch or Bézier surface is a surface extension of a Bézier curve. A Bézier patch is a function of two variables with an array of control points.

A constraint enforced by reaction terms affecting both equations in a constraint of the type u1 = u2. Symmetric constraints are an important special case. See also reaction terms and constraint.

Boolean operations are used to construct a geometry object from other geometry objects. At least two primary geometry objects are required to create a resultant new geometry object. That new object depends on the type of Boolean operation:

A geometric entity with a dimension one less than the space dimension for the geometry (a face in a 3D geometry, an edge in a 2D geometry, and a vertex in a 1D geometry). In a mathematical context, the symbol ∂Ω represents the boundary of the domain Ω . Sometimes boundary is used in a narrower sense meaning an exterior boundary. See also interior boundary, exterior boundary.

See Galerkin boundary element method.

A geometry modeling method to create a geometry by defining its boundaries. Compare to solid modeling and surface modeling.

See hexahedral element.

A memory-saving version of LU factorization where U is the transpose of L. It requires that the coefficient matrix A (A = LU) be a symmetric positive definite matrix. See also LU factorization and positive definiteness.

See nonlocal coupling.

The geometric model of the component on which the physics settings are applied.

Geometric objects made up by combining primitive geometry objects and other composite objects. See also constructive solid geometry, primitive geometry object, and Boolean operations.

For each application launched from a COMSOL Server ™ installation, a separate COMSOL Application Server process is started to run the application. A COMSOL Application Server process contains functionality that is similar to a COMSOL Multiphysics Server together with functionality to generate the application’s user interface accessed from a web browser or a COMSOL Client.

A Windows® client that runs an implementation of a COMSOL application, created with the Application Builder, and that connects to a COMSOL Server™.

The COMSOL Desktop® is an integrated simulation environment for the COMSOL products with a number of windows such as the Model Builder window, the Graphics window, and each model tree node’s Settings window.

A binary data file with the extension .mphbin that contains geometry objects or mesh objects.

A text data file with the extension .mphtxt that contains geometry objects or mesh objects.

A COMSOL Server™ license make it possible to deploy and run COMSOL applications in major web browsers. Using the Windows® operating system, you can also run COMSOL applications by connecting to a COMSOL Server with an COMSOL Client.

A measure of the possible error in a solution due to ill-conditioning of the equations. See also ill-conditioning.

A named model property that has a constant numeric value. The built-in constants in COMSOL Multiphysics include mathematical and numerical constants and physical constants.

Restriction imposed on the dependent variables on the form R(u1,u2,...) = 0. A Dirichlet boundary condition is a special case. Neumann boundary conditions are not regarded as constraints. When a constraint is added, the finite element algorithm adds corresponding reaction terms to the system of equations. These generalized reaction forces modify the flux conditions so that the resulting model becomes solvable.

A solid-modeling method that combines simple solid shapes, or primitives, to build more complex models using Boolean operations. See also solid modeling and primitive.

A boundary condition or source is contributing when it adds to other boundary conditions or sources defined on the same geometric entity. Examples of contributing boundary conditions are loads in structural mechanics and heat flux components in heat transfer. See also exclusive nodes.

Bézier and NURBS curves and surfaces are defined by a set of points known as control points. The locations of these points control the curve’s shape.

Scalar values assigned to control points to further control the shape of a curve or surface.

See vector element.

The path of a point moving through space. See also Bézier curve, NURBS, and manifold.

A geometry object consisting of only edges and vertices (where no vertex is isolated), for example, a geometry object representing a curve.

An individual polynomial or rational polynomial curve. Compounded curves consist of several curve segments.

See mesh element.

One of the unknowns in a discretized finite element model. A degree of freedom is defined by a name and a node point. The degree of freedom names often coincide with the names of the dependent variables. The local degrees of freedom are all degrees of freedom whose node points are in one mesh element.

A geometry where the shape changes with a moving-mesh algorithm. It is also the name of a physics interface for modeling deforming geometries. This is similar to the Parameterized Geometry interface in earlier versions of COMSOL Multiphysics.

A varying quantity whose changes are arbitrary but regarded as produced by changes in other variables on which the varying quantity depends. For example, temperature is a function of the spatial coordinates and time. In a narrower sense, the dependent variables, or solution components, are the unknowns in a mathematical PDE model. Compare to independent variable.

A set of equations that includes both differential and algebraic equations. A DAE is classified in terms of its index, a positive integer, which is related to the minimum number of differentiations needed to transform a DAE to an ODE form.

A solver for a system of linear equations that uses some variant of Gaussian elimination. Compare to iterative solver.

A Dirichlet boundary condition specifies the value of the function (dependent variable) on a boundary. Dirichlet boundary conditions are sometimes called essential boundary conditions or constraints. See also constraint.

A topological part of the modeling space in a geometric model. The geometric representation of a domain is a line segment (interval) in 1D, an area in 2D, and a volume in 3D. In a mathematical context, the symbol Ω represents the domain where the equations are defined.

A nonnegative scalar used in the incomplete LU preconditioner for the iterative solvers. See incomplete LU factorization.

See time-dependent model.

A geometric entity representing a bounded part of a curve. An edge or edge segment is a boundary in a 2D geometry. See also domain.

See vector element.

A PDE that describes an eigenvalue problem with unknown eigenmodes (eigenfunctions) u and eigenvalues λ. The coefficient form eigenvalue PDE is:

where c is positive or negative definite (for example, Poisson’s equation).

To insert a 2D geometry into a 3D geometry sequence.

Deviations from the correct solution, primarily due to: poor modeling; discretization (such as insufficiently fine mesh, poor elements, or insufficiently short time steps); and roundoff and truncation (depending on numerical representation, ill-conditioning, or the solution algorithms).

An estimation of the error in the numeric solution to a problem, either locally or globally, primarily for use by an adaptive mesh refinement. See also adaptive mesh refinement, error.

Boundaries that are rigid transformations of each other and have compatible meshes. See also periodic boundary condition.

See Dirichlet boundary condition.

An Eulerian formulation means that the partial differential equations that describe some physics are formulated in a spatial frame (coordinate system), with coordinate axes fixed in space. An Eulerian formulation is common for fluid flow when the focus is on specific locations in space through which fluid flows. Compare to Lagrangian formulation.

A boundary condition or material model in a domain is exclusive when there can only be one such node defined for a given geometric entity. Adding another exclusive boundary condition to the same boundary, for example, the last added boundary condition (last in the Model Builder tree) overrides any other similar boundary condition defined on the same boundary. Examples of exclusive boundary conditions are prescribed displacements in structural mechanics and specified temperature in heat transfer. See also contributing node.

A data structure that includes the full finite element mesh. See also mesh, node point.

A model that includes nonlocal couplings and dependencies between variables, where the value at a point is the result of a computation elsewhere in the domain or in another geometry defined in the same model. Coupling operators provide the ability to project or extrude values from one geometry or domain to another. Compare to multiphysics.

An exterior boundary for a dependent variable u is a boundary such that u is defined only on one of the adjacent domains, that is, a boundary to the computational domain. See also boundary.

To create a 3D geometry object from a 2D geometry object in a work plane or a planar face in 3D by translating (extruding) it in the normal direction.

A geometric entity describing a bounded part of a surface in a 3D geometry. A face is a boundary in a 3D geometry. See also domain.

See finite element method.

Dependent variables and variables derived from them, defined as fields — functions of x, y, z, and t in a general time-dependent 3D case.

The resulting geometric model that can be used for assigning materials and physics. COMSOL Multiphysics creates the finalized geometry by forming a union of the geometry objects defined in the geometry sequence or by forming an assembly where the geometry objects are treated as individual parts. The finalized geometry consists of one object only.

Only for meshes that define their own geometric model. This geometric model can be used for assigning materials and physics.

In the mathematical sense, a mesh element together with a set of shape functions and corresponding degrees of freedom. The linear combinations of the shape functions form a space of functions called the finite element space. In the traditional FEA sense, the concept of a finite element also includes the discretized form of the PDEs that govern the physics. COMSOL generally uses finite element in the mathematical sense.

A computer-based analysis method for field problems using the finite element method.

A computational method that subdivides an object into very small but finite-size elements. The physics of one element is approximately described by a finite number of degrees of freedom (DOFs). Each element is assigned a set of characteristic equations (describing physical properties, boundary conditions, and imposed forces), which are then solved as a set of simultaneous equations to predict the object’s behavior.

The linear space of functions where the finite element approximation to the solution of a PDE problem is sought. The functions in the finite element space are linear combinations of basis functions (shape functions).

A computation method that, in ways similar to the finite element method, computes values at discrete places on a meshed geometry. Finite volume refers to the small volume surrounding each node point in a mesh.

A finite volume in the geometry that is not defined as a solid domain and that cannot contain a volumetric finite element mesh; only physics interfaces based on the boundary element method can be active in finite voids.

A boundary condition that specifies the value of the normal flux across a boundary, also known as a natural boundary condition. A (generalized) Neumann boundary condition is a special case.

The general flux vector is as below, with three terms: the first term describes diffusion, the second term describes convection with a velocity −α, and the third term γ is a source term. See also generalized Neumann boundary condition and normal flux.

A frame is a coordinate system that is fixed in space, to a material, to the geometry, or to a mesh. The frames make it possible to use an Eulerian formulation or a Lagrangian formulation for various physics in a model or using the arbitrary Lagrangian-Eulerian (ALE) method. The following frame types are available: material frame (reference frame), geometry frame, mesh frame, and spatial frame.

COMSOL Multiphysics supports user-defined functions, which can be analytic, piecewise, and interpolation functions as well as special types of common functions that implement, for example, steps, ramps, and other wave forms. There are also common built-in mathematical functions such as trigonometric functions, logarithms, and special functions.

A Gauss point is an integration point in the special case of numerical integration using Gaussian quadrature. Sometimes, Gauss point is improperly used as a synonym for integration point. See also integration point.

A generalized Neumann boundary condition (also called a mixed boundary condition or a Robin boundary condition) specifies the value of a linear combination of the normal flux and the dependent variables on a boundary. For a coefficient form PDE, the generalized Neumann boundary condition is

The generalized Neumann condition is often called just Neumann condition in the documentation.

see reaction term.

The basic parts that constitute the geometric model and define its position and shape: In 3D, they are divided into the following four types or geometric entity levels: domains, boundaries (faces), edges, and points (vertices). In 2D, there are no faces, and the edges are the boundaries. In 1D, there are only domains and points, which are also the boundaries.

The geometric entity levels are the vertex, edge, face, and domain levels (in 3D). An entity of dimension one less than the space dimension is referred to as a boundary. See also geometric entities.

A collection of geometric entities, their geometric shape, and their connection to each other. Each geometry sequence defines a geometric model. Each meshing sequence that is not conforming with the geometric model of a geometry sequence also defines a geometric model.

A geometric multigrid solver or preconditioner performs one or more cycles of a multigrid method, using a coarsening of the discretization based on a coarsening of the mesh or a reduction in the order of the shape functions. Compare to algebraic multigrid (AMG).

In the geometry frame (coordinate system), the domain is fixed and identical to the original geometry. No physics is formulated directly in the geometry frame — only the material frame and spatial frame have physical significance. The geometry frame is used only as a reference for the Deformed Geometry interface and for postprocessing. When there is no Deformed Geometry interface present, the geometry frame is identical to the material frame.

An object generated by a geometry feature. See also point object, curve object, surface object, primitive geometry object, solid object, and mixed object.

The sequence of geometry features that define a geometric model. In the Model Builder, this is represented by the Geometry node and its child nodes.

A grid usually refers to sets of evenly-spaced parallel lines at particular angles to each other in a plane, or the intersections of such lines. Compare to mesh.

A finite element similar to the Lagrange element. The difference is that there are degrees of freedom for the (first-order) space derivatives at the mesh vertices. See also Lagrange element.

A 3D mesh element with eight corners and six faces, also referred to as brick element; sometimes also called hex element as a short form.

A finite element with basis functions that consists of polynomials of degree 2 or higher.

Creating a geometry by using a combination of boundary modeling/surface modeling and solid modeling.

where ea and c are positive.

An IGES file contains 3D CAD data, including the 3D geometry, in an open format according to the Initial Graphics Exchange Specification. IGES files can be imported into COMSOL Multiphysics using the CAD Import Module.

An ill-conditioned system is sensitive to small changes in the inputs and is susceptible to roundoff errors. See also condition number.

An imprint of the usually smaller boundary on the larger boundary that makes the parts in a pair match. An imprint inserts points on the boundary in 2D and creates edges on the boundary in 3D.

An approximate LU factorization where small matrix elements are discarded to save memory and computation time. The drop tolerance is a relative measure of the smallness of the elements that should be discarded. See also LU factorization.

A variable that can cause variation in a second, dependent variable. The independent variables are most often spatial coordinates and time. Compare to dependent variable.

See differential-algebraic equation.

A single unbounded region, surrounding the geometry, that cannot contain a volumetric finite element mesh; only physics interfaces based on the boundary element method can be active in an infinite void.

The starting values for the dependent variables in a time-dependent analysis and for nonlinear iterations or other iterative solvers.

The order (a nonnegative integer) in a numerical integration formula where evaluation points and weights are chosen such that result of the numerical integration is exact for all expressions that are polynomials of an order that is no higher than the specified integration order.

See numerical integration formula.

An interior boundary for a dependent variable u is a boundary such that u is defined on both adjacent domains or in no adjacent domain. See also boundary.

An interior mesh boundary is the set of mesh faces or mesh edges between mesh elements within a domain.

The domain between two vertices (points) in a 1D geometry. Also called a domain.

An inverted curved element occurs when a curved mesh element inverts locally when more node points are added to better approximate the shape of the geometry. There are many possible geometrical causes, but the element is often too large compared to the geometry feature size.

A finite element that uses the same shape function for the element shape coordinates as for the dependent variables.

See iterative solver.

A solver for a system of linear equations that uses an iterative method, calculating a sequence of more and more accurate approximations to the solution. Each step in this sequence is one linear iteration. This should not be confused with the Newtons iterations (nonlinear iterations) that occur in the solution of a nonlinear system of equations. Compare to direct solver and nonlinear iteration.

A matrix containing the first derivative of a vector-valued function of a vector variable. In particular, it is the derivative of the residual vector with respect to the solution vector. When used in this narrower sense, the term stiffness matrix is sometimes used.

A finite element with polynomial shape functions of a certain order (degree). The value of the function is used as the degree of freedom, and the node points are the Lagrange points.

An extra dependent variable introduced in the flux conditions when a constraint is added. The Lagrange multiplier often has a physical meaning and an interpretation as a (generalized) reaction force. See also constraint.

In a mesh element, the Lagrange points of order k are the points whose local (element) coordinates are integer multiples of 1/k. These points are used as node points for the Lagrange element. For example, the Lagrange points of order 1 are the corners of the mesh element.

A Lagrangian formulation means that the partial differential equations that describe some physics are formulated in a material frame (coordinate system) with coordinate axes fixed to the material in its reference configuration and following the material as it deforms. The Lagrangian formulation is common for solid mechanics because it makes anisotropic material properties independent of the current spatial orientation of the material. Compare to Eulerian formulation.

A step in a linear iterative solver. See iterative solver. Compare to nonlinear iteration.

An equation where both sides are sums of a known function, the unknown functions, and their partial derivatives, multiplied by known coefficients that only depend on the independent variables. Other PDEs are called nonlinear.

For a linear system of equations, a version of Gaussian elimination that produces a factorization A = LU of the coefficient matrix, where L and U are the lower and upper triangular matrices, respectively. This makes it easy to quickly solve a number of systems with the same coefficient matrix. See also direct solver.

A structured mesh with quadrilateral elements generated by mapping using transfinite interpolation.

The mesh generator creating mapped meshes.

The matrix E that multiplies the second time derivative of the solution vector in the linearized discretized form of a PDE problem. If there are no second time derivatives (that is, if E = 0), then the term mass matrix is often used for the matrix D that multiplies the first derivative of the solution vector (the D matrix is otherwise called the damping matrix).

The material frame defines a coordinate system that is fixed to the material in its reference configuration and follows the material as it deforms. The material frame is used in connection with a Lagrangian formulation. This frame is also referred to as a reference frame.

Built-in common mathematical constants such as π and i and numerical constants such as the machine precision or machine epsilon.

A subdivision of the entities of a geometric model into, for example, triangles (2D) or tetrahedra (3D). These are examples of mesh elements. See also grid, structured mesh, and unstructured mesh.

The individual elements in the mesh that together form a partitioning of the geometry, for example, triangular elements and tetrahedral elements. See also finite element. A curved mesh element is a mesh element that is extended with additional node points to better approximate the shape of the geometry.

In the mesh frame (coordinate system), the domain is fixed until an automatic or manual remeshing operation is performed, as well as between remeshing events. When remeshing is not used, the mesh frame is identical to the geometry frame.

An endpoint or corner of a mesh element. See also node point and vertex.

The mesh generator. There are operations to create both structured mesh and unstructured mesh.

The sequence of mesh features that builds a mesh. In the Model Builder, this is represented by the Mesh node and its child nodes. The mesh can either be conforming with the component's geometry, or define its own geometric model.

See generalized Neumann boundary condition.

A nonempty geometry object that is not a solid object, surface object, curve object, or point object. For example, the union of a solid object and a curve object is a mixed object.

A model-reduction technique for reducing systems with many degrees of freedom, such as large finite element models, to a form with fewer degrees of freedom for dynamic system simulations and analysis. See also state-space model.

See nonlocal coupling.

Model inputs are fields such as temperature and velocities or other physical properties that act as inputs for material properties and model equations. The model inputs can be fields computed by other physics interfaces or user-defined values.

A file that contains Java® commands calling on the COMSOL API. Use a text editor to extend and modify the model file. Compiling and running a model file for Java creates the COMSOL Multiphysics model.

A text file containing commands that create a COMSOL Multiphysics model. A model file for MATLAB is a text file (M-file) that is similar to a model file for Java and that can be modified and used with MATLAB. If you have a MATLAB license and a license for LiveLink™ for MATLAB®, the COMSOL Desktop can load a model file for MATLAB. Compare with Model MPH-file.

A binary data file with the extension .mph that contains a COMSOL Multiphysics model or application. Often also just called model file or application file.

Magnet resonance imaging (MRI) data is an image data format, primarily for medical use. MRI produces high-quality images of the inside of the human body. 3D MRI data is usually represented as a sequence of 2D images.

A solver or preconditioner for a linear system of equations that computes a sequence of increasingly accurate approximations of the solution by using a hierarchy of coarsened versions of the linear system (having fewer degrees of freedom). See also algebraic multigrid, geometric multigrid.

Multiphysics models include more than one equation and variable from different types of physics. These variables can be defined in different domains. The equations can be coupled together through equation coefficients that depend on variables from other equations. Compare to extended multiphysics.

See Neumann boundary condition.

A Neumann boundary condition specifies the value of the normal flux across a boundary. Neumann boundary conditions are sometimes called natural boundary conditions. Compare to generalized Neumann conditions.

An iterative solver method, also called the Newton-Raphson method, for solving nonlinear equations. See also nonlinear iterations.

See Newton’s method.

Any point in the mesh element where the degrees of freedom are defined. The node points often include the mesh vertices and possibly interior or midpoint locations. See also degree of freedom (DOF) and mesh vertex.

A Newton step in the solution of a nonlinear PDE problem. Each nonlinear iteration involves the solution of a linear system of equations. Compare to linear iteration.

See linear PDE.

User-defined nonlocal couplings are used to couple data within a model component (geometry) or between different model components (geometries). See also extrusion nonlocal coupling, projection nonlocal coupling, and integration nonlocal coupling. Nonlocal couplings can be reused with different arguments (for example, for integrating different quantities over the same domain).

A numerical integration method that approximates an integral by taking the weighted sum of the integrand evaluated at a finite number of points, the integration points (sometimes improperly called Gauss points). Also called quadrature formula.

The normal component of the flux vector at a boundary.

The nonuniform rational B-spline (NURBS) is a curve and surface representation scheme. A NURBS representation can be divided into a number of rational Bézier curves or surfaces.

In the context of model reduction, online refers to using the reduced order for evaluations rather than producing them.

A user-defined operator function, or just operator, is similar to a function but behaves differently. For example, COMSOL Multiphysics includes differentiation operators that take expressions as input arguments to define a derivative of an expression with respect to a variable. There are also built-in arithmetic, relational, and logical operators.

The degree of the polynomials that define the shape functions (basis functions).

An equation involving functions and their derivatives. The derivatives are with respect to one independent variable only. Compare to partial differential equation (PDE).

where da and c are positive.

A constant that can take on different values for each model in a parametric analysis. See also constant.

An equation involving functions and their partial derivatives; that is, an equation that includes derivatives with respect to more than one independent variable. Compare to ordinary differential equation (ODE).

A boundary condition where the values of the solution appear in a periodic pattern, typically so that the value of the solution on one boundary is equal to the value on another boundary. See also equivalent boundaries.

Sets of physics nodes for different types of physics in the COMSOL Desktop environment. The physics interfaces (sometimes referred to as the physics) contain predefined equations and boundary conditions and a set of nodes for setting up models for that type of physics.

Usually a value on the main diagonal of the stiffness matrix. Pivoting is the interchanging of rows and columns in order to place a particularly large element in the diagonal position. The value of the diagonal element when it is used to eliminate values below it is called the pivot value.

A location in space. Often used in a narrower sense with the same meaning as vertex.

A geometry object with only vertices.

A symmetric matrix is positive definite when all its eigenvalues are positive.

The convergence rate of iterative methods depends on the spectral properties of the coefficient matrix. A preconditioner is a matrix that transforms the linear system into one that has the same solution but that has more favorable spectral properties. See also algebraic multigrid, geometric multigrid, incomplete LU factorization, iterative solver, and SSOR.

A geometry object with a basic shape such as a cube or a sphere. Add primitives to a model, using arbitrary sizes and positions, and combine them to form complex shapes. See also constructive solid geometry, composite geometry object, and Boolean operations.

A 3D mesh element with six corners and five faces, also referred to as wedge element.

See numerical integration formula.

A 2D mesh element with four corners and four edges; sometimes also called quad element as a short form.

See Bézier curve.

see reaction term.

Terms that are automatically added to the system of equations in order to enforce a constraint. Reaction terms from boundary constraints appear as a flux condition and share the same physical meaning. Using an analogy from structural mechanics, reaction terms are sometimes referred to as (generalized) reaction forces.

See material frame.

The vector L in the discretized form of a PDE problem. In the absence of constraints, the discrete form of a stationary equation is 0 = L(U) where U is the solution vector.

See generalized Neumann boundary condition.

A basis function described in local element coordinates. See also basis function.

A value σ around which an eigensolver searches for eigenvalues.

Triangle element in 2D and tetrahedral element in 3D.

See solid object.

A 3D geometry modeling method that describes both the boundary and interior of the geometry using solid objects. See also constructive solid geometry (CSG) and solid object.

A geometry object whose vertices, edges, and faces all have an adjacent domain.

See dependent variable.

A matrix that contains a sequence of solutions as columns. A steady-state problem results in a solution vector, but eigenvalue problems, time-dependent problems, and parametric analyses produce a solution matrix.

A vector with components that contain all the degrees of freedom (values of the dependent variables) as its components. See also solution matrix.

The spatial frame defines a coordinate system with coordinate axes fixed in space. The spatial frame (also called the Eulerian frame) is used in connection with a Eulerian formulation.

A solver for a time-dependent model is unconditionally stable if the initial conditions are not amplified artificially and the roundoff errors do not grow, regardless of the size of the time step. A solver is conditionally stable if there is a maximum value of the time step above which the numerical solution is unstable.

A linear time-invariant representation of a dynamic system as a set of first-order ODEs of the form

where x is the state vector, u is the input, and y is the output. A, B, C, and D are the constant dynamics, input, output, and direct transmission matrices, respectively.

See stationary model.

A model where the dependent variables do not change over time. It typically represents a steady-state solution. Also called static model or steady model.

See stationary model.

See Jacobian matrix.

The locus of particles that have earlier passed through a prescribed point in space. See also streamline.

A curve that is tangent to the vector field everywhere (in particular a velocity field) at a given instant of time. Sometimes called a flow line or flux line. See also streakline.

A numerical technique for stabilization of the numeric solution to a PDE by artificially adding diffusion in the direction of the streamlines.

A partial differential equation in the strong form is the standard formulation as an equality of functions. The strong form is divided into the coefficient form and the general form. Compare to coefficient form, general form, and weak form.

A mesh for which all elements and nodes have the same topology. Compare to unstructured mesh.

A 3D geometry modeling method to describe a geometry by defining its bounding surfaces. Compare to boundary modeling and solid modeling.

A 3D mesh generated by sweeping a face mesh along a domain, creating a mesh that is structured in the sweep direction. Compare to structured mesh.

Mesh generator creating a swept mesh.

A symmetric successive overrelaxation (SSOR) preconditioner uses classic SSOR iterations.

The invariance of an object attribute or of the object itself under a transformation such as inversion, rotation, or reflection. A symmetry allows for a reduction of the model geometry so that appropriate boundary conditions account for the redundant portions of the geometry. Axial symmetry is a common type of symmetry.

A constraint that is enforced by reaction terms chosen so as to preserve the symmetry of symmetric unconstrained systems. This choice of reaction terms is unique and leads to a bidirectional constraint that modifies the equations corresponding to all dependent variables appearing in the constrained expression.

See equivalent boundaries.

See weak form.

The mesh generator creating unstructured tetrahedral meshes. See unstructured mesh.

See transient model.

A model where at least one of the dependent variables changes over time, for example, the heat equation or the wave equation. Also called dynamic model, time-dependent model, or unsteady model.

The mesh generator creating unstructured triangular meshes. See unstructured mesh.

If the parameter space of a surface is divided into “valid” and “invalid” regions, the image of the valid regions is called the trimmed surface. This corresponds to the part of the surface limited by a closed loop of edges lying on the surface.

A constraint enforced by reaction terms that only affect one of the dependent variables in a constraint of type u1 = u2. The other dependent variables are treated as independent with respect to the unidirectional constraint. Compare to symmetric constraint. See also constraint.

A mesh without a specific pattern where the elements can have different shapes and the nodes can have different connectivities. An unstructured mesh can represent any geometry and can be created using a triangle mesher, a quad mesher, or a tet mesher. Compare to structured mesh and mapped mesh.

See time-dependent model.

A user-defined variable can be defined on a global level or on any geometric entity in terms of dependent variables, independent variables, parameters, constants, and other variables.

A finite element often used for electromagnetic vector fields. Each mesh element has degrees of freedom corresponding only to tangential components of the field. Also called curl element, Nédélec’s edge element, or just edge element.

A point in a geometric model, often an endpoint of an edge or an intersection of geometric entities of a higher degree such as edges or faces. A vertex is referred to as a point for the specification of point sources and other PDE modeling. See also domain.

A reformulation of a constraint as a weak form equation. When using a weak constraint, the corresponding Lagrange multiplier becomes a solution component (dependent variable).

A partial differential equation in the weak form is a more general formulation than the strong form. It is produced by multiplying the strong form PDE with an arbitrary function called the test function and integrating over the computational domain. Physics interfaces in COMSOL Multiphysics are implemented using a weak form. Compare to strong form.

See prism element.

An embedded 2D workspace that can be positioned relative to the coordinate planes or an already existing 3D geometry. Using work planes makes it possible to define a geometry in terms of previously created geometry objects such as points, edges, and faces. From a work plane with a 2D geometry, 3D geometry objects can be created using extrude or revolve operations.