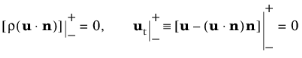This condition properly accounts for a sudden jump in porosity εp across boundary between different domains, giving the corresponding jump in stress across the interface. The emergence of a boundary layer on the upstream side of the interface is also revealed, which provides modifications to the behavior of the tangential velocity near the interface. The feature helps to avoid the need to add a very thin transition region, in which εp,upstream changes to εp,downstream continuously, while solving the Brinkman equation in such situations. Below, ‘−’ and ‘+’ (used as subscripts and superscripts) refer to the upstream and downstream side of the interface, respectively.

Whatever the option for Continuity conditions is chosen, the velocity conditions are

That is, the mass flux and tangential velocity across the interface are constant, and n is assumed to be a normal pointing from ‘−’ to ‘+’. Velocity and stress option just imposes usual stress continuity adding a correction for a possible jump in density:

The option Velocity and porosity-corrected stress (default) adds a contribution due to the inertial term, which is non-trivial (gives non-zero effect) when εp jumps across the interface:

Then, the Velocity and porosity-corrected stress with loss option has a ‘pressure loss’ term:

This loss occurs in the downstream direction. Its mechanism is similar to the mechanism of common engineering ‘total pressure loss’. Indeed, ‘expansion’ and ‘contraction’ across the interface experienced by the flow on the microscopic level (due to increasing or decreasing porosity, εp, respectively), are roughly equivalent to expansion and contraction of flow in a pipe with geometrical variations. Accordingly, it is assumed that only the normal velocity component is responsible for the loss. In the case of normal flow and negligible viscous term the pipe-analogy is quite exact.

Subsequently, Pressure loss model should be specified. Choosing User-defined loss coefficients requires values of Expansion loss coefficient and Contraction loss coefficient (Kexp = 1 and Kcontr = 0.5 are default values). The resulting losses on the ‘expansion’ and ‘contraction’ boundaries are:

Borda–Carnot option results in the following losses:

and requires to choose Vena contracta model. The User defined option asks for value of Vena contracta coefficient (cvc = 0.5 by default). Weisbach option computes the coefficient based on the ratio of porosities across the interface:

and requires inputs for Lower limit and Exponent (cvc,ll = 0.63 and nvc  = 3 are default values).

Although the velocity conditions formally look the same for all Continuity conditions options, the latter two (containing the inertial correction due to the porosity jump) lead to an extra non-trivial effect. Namely, the tangential velocity exponentially evolves over a boundary layer formed on the upstream side of the interface boundary. This boundary layer has a characteristic length equal to

In terms of the interstitial velocity, u(i) =  u/εp, this results in:

Obviously, tangential component of the interstitial kinetic energy is lost across the interface. For low viscosity and high normal-flow component, when lu is much lower than lgeom (the characteristic geometry length) there are apparent variations in ut and u(i)t in a thin boundary layer on the upstream side of the interface. However, for the cases with high viscosity or nearly interface-parallel flow, lu is much larger than lgeom, and any variations in ut and u(i)t are virtually invisible.

Notice that the feature does not take into account possible underresolved porous scale, as is described in Theory for the Free and Porous Media Flow, Darcy Interface.