The gravity force is defined from the acceleration of gravity vector, g, and the density,
ρ. Under usual conditions and in Cartesian coordinates with the
z-axis in the vertical direction,
When gravity is considered, a volume force equal to ρg is included in the momentum equation. For example, for laminar weakly compressible flow, it reads:
Introducing a constant reference density ρref, and assuming that
g is homogeneous, this equation is equivalently written:
where r is the position vector and
rref is an arbitrary reference position vector.
In Equation 13-12, the gravity force is written
(ρ − ρref)g.
When the relative pressure is used (default option) the interface dependent variable represents the relative pressure and the absolute pressure is defined as pA = pref + p. When the pressure is used to define a boundary condition (for example, when
p0 defines the pressure condition at an outlet), it represents the relative pressure. Hence defining the outlet pressure as
phydro,approx = −ρrefg ⋅ (r − rref) compensates for the gravity force for an ambient reference pressure of 0 Pa when the density is constant, there is no external force, and provided
pref,
g, and
r0 are defined consistently.
When the reduced pressure is used, the interface dependent variable (named p by default) represents the reduced pressure. The absolute pressure is then defined as
pA = pref − ρrefg ⋅ (r − rref) + p. In this case when the pressure is used to define a boundary condition (for example, to define a pressure condition at an outlet), its value corresponds to the reduced pressure. Hence, the prescribed pressure compensates for an approximate hydrostatic pressure,
phydro,approx = −ρrefg ⋅ (r − rref), which is exact only when the density is constant and there is no external force.
.
.
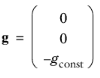depending on the pressure formulation.