Use a Rotated System () to define an orthonormal coordinate system which is rotated with respect to the reference system. In 2D, you can specify either an in-plane rotation angle or a full 3D rotation using Euler angles. The rotation is intrinsic.

Full 3D rotations are specified as three consecutive Euler angles α, β, and γ. Rotation axes and angles are illustrated in Figure 5-5 where the resulting rotated system axes are denoted X, Y, and Z.

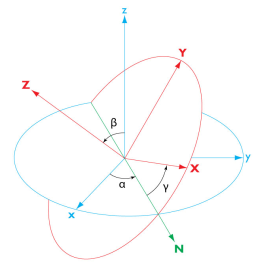
The transformation matrix defined by the Euler angles transforms components of a fixed vector v from the rotated coordinate system, [vX,vY,vZ], to components in the global system, [vx,vy,vz], as follows:

If this coordinate system is added as a subnode to a Combined System node, define where it will be active using a selection in the Geometric Entity Selection section. Also, the Name and Coordinate names fields are not available in this case.

In the Coordinate Names table, the default names appear in the First, Second, and Third columns — x1, x2, and x3. In planar 2D models, x1 and x2 are typically the in-plane coordinates, and x3 is the out-of-plane coordinate. Change the names if desired.

The rotation settings depend on the space dimension of the component to which the coordinate system belongs. For 2D components, first select an Input method: In-plane rotation (the default) or General rotation.

When the input method is set to In-plane rotation in a 2D component, you specify the rotation as a single angle (in radians) representing the Rotation about out-of-plane axis. The Out-of-plane axis can be set to any of the three main axes, pointing either into or out of the screen. The default for planar 2D geometries is Third out-of screen, which leaves the x and y axes as in-plane reference axes. For axisymmetric geometries, the default is Second out-of screen, leaving the r and z axes in-plane.

For 3D geometries and when General rotation has been chosen as input method in 2D, then, under Euler angles, choose a sequence of Euler angles from the Rotation sequence list; the default is Z-X-Z, which corresponds to sequential rotation first about the z-axis, then the x-axis, and finally the z-axis again. Enter the angles (in radians) in the α, β, and γ fields (see the graphics in the Settings window for definitions of these angles). The default values are 0 for all angles.

Specify the location of the Origin of the base vector coordinate system in the global Cartesian system. The default is an origin coinciding with the one from the global system using the frame chosen from the Frame list (default: Spatial).

From the Work plane list, select xy-plane (the default, for a standard global Cartesian coordinate system) or select any work plane in the geometry sequence. If you choose a work plane, the work plane’s coordinates xw, yw, and zw are used for the definition of the rotated system.