The Gaussian Pulse function () is the common bell-shaped curve (Gaussian function). It has a shape that is similar to a Gaussian (normal) distribution. The default Function name is gp1.

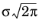
In the equation above, x is the input variable, x0 is the location (mean), and σ is the standard deviation. The normalization factor n is equal to 1 for peak value normalization and for integral normalization. This function is a function of one variable (the time t, for example). If desired, a baseline value (other than zero) can be added to the function value.

Enter a Location value for the Gaussian pulse mean x0 (the default location is 0). Enter a Standard deviation σ of the normal distribution. The default is 1. You can also enter a Baseline for the pulse function (default: 0). Choose a Normalization method: Integral (the default) or Peak value. With the default method, you can enter an Integral value (default: 1). The latter option can be useful if the maximum value of the pulse becomes very large, which may upset nonlinear equations. You can then choose an Peak value to normalize the Gaussian pulse so that its maximum, rather than its integral, is 1. You can use unit syntax to assign units to these parameters.