The Packed Bed Feature
The Packed Bed feature, available to users of the Chemical Reaction Engineering Module, adds a domain feature that can simulate regions filled with reactive porous pellets, as in packed bed reactors. The theory for the Packed Bed feature available in the Transport of Diluted Species interface is presented below.
The pellets in the bed are simulated with the Extra Dimension technology provided by the COMSOL software: A 1D, 2D, or 3D domain represents the bed volume. The extra dimension is the added radial microscale dimension inside each pellet.
There are two types of pellets, acting as porous catalyst and reactant (Shrinking Core) respectively. For the porous catalyst pellet, the whole radius is mapped to the extra dimension, while for the Shrinking Core pellet, the radial length of porous reacted outer-layer is mapped to the extra dimension.
pellet: porous catalyst
The species diffuse from packed bed into porous pellet where they go through catalytic reactions, then diffuse back into the packed bed.
For an example of how to use the Packed Bed, see the model example A Multiscale 3D Packed Bed Reactor, file path Chemical_Reaction_Engineering_Module/Reactors_with_Porous_Catalysts/packed_bed_reactor_3d
Figure 3-3: Schematic showing the macroscale (bed volume) and the microscale (pellet).
The transport and reaction equations inside the pellets are solved on an extra dimension attached to the 1D, 2D, or 3D physics interfaces, including axisymmetric cases.
The equations inside the spherical pellet are solved as spherical transport equations on nondimensional radial coordinates on the domain 0-1.
The model equations assume spherical particles (pellets) of a radius rpe. Modeling assumptions for cylinders, flakes, and user-defined shapes can also be used. Consider the microscale concentration cpe inside an individual porous pellet or pellets, and the macro-concentration c in the packed bed gas volume.
The pellet radius input can be:
The model equation for the bulk (macroscale) species is, for example:
(3-21)
•
εb is the bed porosity.
•
The dependent variable c for each chemical species i represents the interparticle concentration, that is, the concentration based on unit volume of fluid flowing between the pellets.
•
Ri is the species interparticle reaction rate in the bed. This corresponds to reactions occurring in the macropores between the pellets in the bed. Note that Ri is the reaction rate per unit volume of bed.
Looking inside a pellet: Assuming no concentration variations in the space-angle (θ, φ) direction, but only in the radial (r) direction of the spherical pellet allows a spherically symmetric reaction-diffusion transport equation inside the pellet. If rdim (SI unit: m) is the spatial radial coordinate in the pellet, and rpe is the pellet radius, the nondimensional coordinate r = rdim/rpe can be defined. The modeling domain on r goes from 0 to 1.
Figure 3-4: Modeling domain in a pellet for dimensional (top) and nondimensional (bottom) coordinates.
A shell mole balance across a spherical shell at radius rdim (SI unit: m), and a subsequent variable substitution r = rdim/rpe gives the following transport equation on the pellet domain 0 < r < 1:
(3-22)
•
εpe is the pellet (microscale) porosity.
•
cpe,i is the intraparticle concentration of species i in moles/m3 of fluid volume inside the micropores.
•
Rpe,i is the pellet reaction rate. This corresponds to reactions taking place inside the pellets. Note that the user input of Rpe,i is per unit volume of pellet.
Assuming that the pellet bed is homogenized, that is that pellets are present in an averaged sense in each point of the geometry, the equation to be solved in the packed bed is:
(3-23)
where N is the number of pellets per unit volume of bed:
Dividing Equation 3-22 by (the pellet area times r2), the governing equation inside each pellet is:
(3-24)
The effective diffusion coefficient in the equations above depends on the porosity εpe, tortuosity τ, and physical gas diffusivity D in the manner of
.
The available models for the porous media tortuosity are the one by Millington and Quirk (Ref. 3),
(3-25),
the Bruggeman model,
(3-26)
and the Tortuosity model, where the tortuosity expression is entered as user defined input.
These are readily used for both gaseous and liquid fluids along with various types of pellet shapes. For instance, the first model has been shown to fit mass transport in soil-vapor and soil-moisture well.
Equation 3-22 can be solved for two types of boundary conditions at the interface between the pellet surface and the fluid in this feature.
•
Continuous concentration: assuming that all resistance to mass transfer to/from the pellet is within the pellet and no resistance to pellet-fluid mass transfer is on the bulk fluid side. The concentration in the fluid will thus be equal to that in the pellet pore just at the pellet surface: . This constraint also automatically ensures flux continuity between the internal pellet domain and the free fluid domain through so-called reaction forces in the finite element formulation.
•
Film resistance (mass flux): The flux of mass across the pellet-fluid interface into the pellet is possibly rate determined on the bulk fluid side by film resistance. The resistance is expressed in terms of a film mass transfer coefficient, hDi, such that:
(3-27),
where Ni, inward is the molar flux from the free fluid into a pellet and has the unit moles/(m2·s).
With the film resistance formulation above, the free fluid Equation 3-21 needs to be amended for flux continuity so that
(3-28)
where Sb (SI unit: m2/m3) is the specific surface area exposed to the free fluid of the packed bed (not including the inside of the pores).
For the case of randomly packed spherical pellets, the specific surface area exposed to the free fluid is (Ref. 15):
(3-29)
The mass transfer coefficient in Equation 3-27 can be computed from the fluid properties and flow characteristics within the porous media. For this, the Sherwood, Sh, number defined as the ratio between the convective mass transfer coefficient and the diffusive mass transfer coefficient is often used:
where L is a characteristic length (for spheres, typically the radius), and D is the diffusion coefficient in the fluid. From the Sherwood number definition, the mass transfer coefficient can be computed.
Three commonly used empirical expressions for the calculation of the Sherwood number are the Frössling relation (Ref. 16):
(3-30),
which was measured on pellets in the size region 1 mm, the Rosner relation (Ref. 17)
(3-31),
and the Garner and Keey relation (Ref. 16)
(3-32),
which was measured for Re numbers greater than 250.
All three depend on the Reynolds, Re, and Schmidt, Sc, numbers. The first describing the fluid flow regime (laminar versus turbulent) and the second, the ratio between the viscous diffusion rate and the molecular (mass) diffusion rate. In the expressions, properties such as velocity, u, dynamic viscosity, μ, and density, ρ, of the fluid are included.
Surface Species
Surface species correspond to species bound to the solid interface within the porous pellet, which is also in contact with the pore fluid. The surface species hence only exists within the pellet. The surface species are assumed to be immobile, and the concentration is only dependent on the reaction rate of surface reactions involving the species:
(3-33)
It can be noted that there is no mass flux of surface species within the pellet or across the pellet outer surface and the bulk fluid. The unit of surface species concentration cpes is amount per area, and the corresponding surface reaction rate unit is amount per area and time.
When surface species are present, the equation governing transport of bulk species inside the each pellet is:
(3-34)
The second term on the right hand side represents species production or removal due to surface reactions in the pellet. It is composed of the reactive specific area Sb,reac, the area per volume available for surface reactions, and the surface reaction rate .
It should be noted that the surface reaction rate for a bulk species and the surface reaction rate for a surface species are related but not identical since the species may represent different molecules.
Nonspherical Particles
For nonspherical pellets (of any shape), the relations above can be applied approximately by reinterpreting the pellet radius rpe as
(3-35)
(Ref. 18), where Vpe and Ape are the volume and external surface, respectively, of a single pellet of any shape. Since the specific surface Spe (SI unit: m2/m3) of one pellet is defined as
it follows by insertion of Equation 3-35 that
.
For a packed bed of which the packing has a porosity εb, the specific surface of the bed will be
or
(3-36)
for any pellet shape. Now rpe and Sb can be calculated for any shape and inserted in equations Equation 3-22 and Equation 3-28. Some common specific shapes have automatic support:
Cylinders
 
For cylindrical shapes, applying Equation 3-35 gives
(3-37).
It is common practice to assume that the top and bottom surface of cylindrical pellets have negligible effect on the mass transfer to and from the internals of the pellet, or, . Equation 3-37 then simplifies to
and Equation 3-36 to
Flakes
 
The derivation for a disc-shaped catalyst pellet is exactly the same as for cylindrical pellets, except that the assumption is reversed about the end surfaces and the envelope surface: , where wflake is the thickness of the disc. This gives
and
.
Surface Reaction
Surface reactions can also be simulated inside the pellet. Surface species are introduced in pellet by adding them in the Surface Species section of the Pellets node available under Packed Bed.
A bulk species can take part in both volumetric and surface reactions. The total reaction rate for a bulk species within a pellet is defined as:
Here Rpe is the reaction rate for bulk reactions occurring inside the pellet. Rpe,s and Sb are the reaction rate and the reactive specific surface area for a surface reaction occurring inside the pellet, on the interface between the solid matrix and the fluid.
Heat Source
The heat source of endothermic or exothermic reactions inside the pellet needs to be accounted for in the heat transfer on the bulk level if the heat balance is not solved within the pellet. Thermal equilibrium is assumed in each pellet, and the source is averaged across the pellet:
(W/m3)
If there are multiple pellet sizes i in the bed the heat source computed by summing over all sizes:
Here θv,i is the volume fraction of pellet i in the pellet mix.
Pellet: Shrinking Core
Species diffuse from packed bed through porous reacted shell layer onto the pellet core surface where they take part in heterogeneous reactions. With the solid species inside pellet core consumed in the reactions, the unreacted core is shrinking, and at the same time the reaction products diffuse through the reacted layer back into the packed bed.
Figure 3-5: Schematic showing Shrinking Core Model.
The core shrinking rate depends on the heterogeneous reaction rate and the properties of pellet,
(3-38)
•
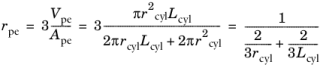rc is the pellet core radius (m)
•
Rsolid is the surface reaction rate (mol/(m2·s)) for solid species
•
Msolid is the solid species molar mass
•
ρpe is the pellet core density
If there are two or more species, the term (RsolidMsolid) is mass weighted, assuming same consuming pace is held along the r direction for all solid species.
The transport and reaction equations inside the porous reacted shell (layer) are solved on a normalized dimensionless extra dimension S (0-1) which is based on the thickness (r) of the reacted layer.
The general form of the mass transport equation inside reacted layer is
The shell mole balance across a spherical shell at radius r (rc <= r <= rpe),
and weak form,
(3-39)
Defining extra dimension coordinate s as
The integration can be written as
(3-40)
For time derivative in moving coordinate system,
(3-41)
On the extra dimension(s), the mass transport equation to be solved inside the reacted layer is (from Equation 3-39, 3-40, and 3-41).
where εpr is the porosity inside the reacted pellet.
For the pellet shapes, diffusion process and heat sources, they are similar to that for porous catalyst pellet. The shape can be both spherical and nonspherical particles, and the characteristics and properties of the pellet are defined in the Pellet node under Porous Material. The heat sources are contributed from the bulk reactions and Shrinking Core reactions (surface reactions).
Shrinking Core Reactions
The pellet core consuming rate depends on the rate of Shrinking Core Reactions, Equation 3-38. The solid species in the pellet core take part in the heterogeneous reactions as reactants. The pellet core is shrinking with the proceedings of the surface reactions. If there are two or more solid species, the shrinking rate is the mass weighted consuming rate, and here it is supposed that all solid species shrinks at the same pace along the radial direction.
Boundary Conditions
Outer Surface
 
There are two types of boundary conditions on interface between the pellet outer surface and the fluid in the bed: Continuous concentration and Film resistance (mass flux). They are the same as that for catalyst pellet.
Core Surface
 
The core consuming reactions always exist on the core surface. Besides the solid species in the pellet core, there could be also bulk transport species that participate in the heterogeneous reactions. The surface reaction rate for the bulk species is a kind of the mass flux (Jpe,i) between the core surface and the porous reacted layer. The mass source for species Cpe,i is
where