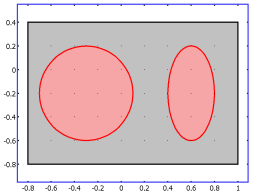
The level set method is a technique to represent moving interfaces or boundaries using a fixed mesh. It is useful for problems where the computational domain can be divided into two domains separated by an interface. Each of the two domains can consist of several parts. Figure 11-2 shows an example where one of the domains consists of two separated parts. The interface is represented by a certain level set or isocontour of a globally defined function, the level set function ϕ. In COMSOL Multiphysics, ϕ is a smooth step function that equals zero (0) in one domain and one (1) in the other. Across the interface, there is a smooth transition from zero to one. The interface is defined by the 0.5 isocontour, or level set, of ϕ. Figure 11-3 shows the level set representation of the interface in Figure 11-2.

The physics interface solves Equation 11-3 in order to move the interface with the velocity field u:

The terms on the left-hand side give the correct motion of the interface, while those on the right-hand side are necessary for numerical stability. The parameter, εls, determines the thickness of the region where ϕ varies smoothly from zero to one and is typically of the same order as the size of the elements of the mesh. By default, εls is constant within each domain and proportional to the largest value of the mesh size, h, within the domain. The parameter γ determines the amount of reinitialization or stabilization of the level set function. It needs to be tuned for each specific problem. If γ is too small, the thickness of the interface might not remain constant and oscillations in ϕ can appear because of numerical instabilities. On the other hand, if γ is too large the interface moves incorrectly. A suitable value for γ is the maximum magnitude of the velocity field u.