Large Eddy Simulations offer an alternative approach to turbulent flow simulations as compared to the RANS approach (see Theory for the Turbulent Flow Interfaces). In LES, the larger three-dimensional, unsteady eddies are resolved, whereas the effect of the smaller eddies is modeled. This requires the simulations to be three-dimensional and time dependent. 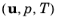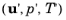The velocity, pressure and temperature fields are divided into resolved, , and unresolved, , scales. The unresolved scales are assumed to be orthogonal to the inner-product space of the resolved scales and to vanish on ∂Ω, the boundaries of the domain Ω, (see Ref. 1 for further details).

Projecting Equation 3-218 onto the finite element subspaces for the resolved pressure, velocity and temperature scales, and neglecting the influence of unresolved scales on the diffusion coefficients for momentum and heat gives

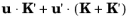
If the pressure and temperature belong to the same inner-product space, the last line of Equation 3-222 becomes a constant multiple of the weak-form continuity equation, which is solved to numerical precision. In the current implementation, the subscale viscous work, , is neglected since cannot be resolved. This results in the following weak-form energy equation:

Here, C1, C3, and C4 are constants depending on the order of the shape functions and the shape of the element, and C2 is a constant depending on the temporal scheme. G is the covariant metric tensor, and k is the thermal-diffusion tensor.

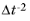
When the Use dynamic subgrid time scale option is selected, the first terms under the square-roots in Equation 3-227 are replaced by estimates of inverse time scales based on time-derivatives of momentum and enthalpy. The Limit small time steps effect on stabilization time scale option is used to ramp out the time-derivative terms in Equation 3-226 and terms proportional to in Equation 3-227 when the time step becomes much smaller than what is required in LES (see Temporal resolution).

In certain cases, the residual-based Reynolds-stress contribution has been found to be too small (see Ref. 2). For this reason, the residual-based variational multiscale with viscosity (RBVMWV) method adds residual-based viscosity terms to the right-hand side of the weak-form momentum and energy equations in Equation 3-219,

where 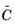is a model constant, and h is a measure of the element size.

and 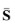is the projection of S onto the space of constant shape functions. This corresponds to a further decomposition of the resolved scales into large resolved scales and small resolved scales (see Ref. 3).

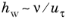
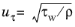
When Wall treatment is set to Low Re, a Dirichlet condition is imposed on the velocity field at the walls. Adequate resolution of the wall layers requires that , where hw is the thickness of the mesh cells next to the wall and is the friction velocity based on the tangential stress τw at the wall.

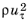
When Wall treatment is set to Automatic, a Dirichlet condition is imposed on the wall-normal velocity component and a traction force is applied in the tangential direction opposite to the local velocity vector. To evaluate the magnitude, , of the traction force, the Reynolds number based on the magnitude of the tangential velocity and the normal distance, y, to the wall,

is evaluated halfway between the wall and the first vertexes inside the domain, at y = δw. Asymptotic solutions to the L-VEL equation (Equation 3-75) can be found for low and high values of the Reynolds number. For low values of the Reynolds number (inside the viscous wall layer),

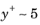
The Automatic option should be used with caution since boundary layers, especially on smooth surfaces, in many cases need to be resolved down to the top of the viscous wall layer (). When the point of boundary-layer separation is known, such as for the flow around bodies with sharp edges, the Automatic option may be used to reduce the number of DOFs in the model. Automatic wall treatment for the energy equation is described in

When automatic wall treatment is applied in an LES model, a flux condition is imposed for the energy equation. The heat flux between the fluid with temperature Tf and a wall with temperature Tw, is

where T+ is the dimensionless temperature, given by

where hU is the mesh size in the streamline direction. Larger values of Δt may lead to damping of turbulence and in some cases even convergence issues. The built-in variable spf.dt_CFL may be used to limit the maximum time step.