Over a boundary between a free flow and a porous domain, the macroscopic saturation of the different phases is often discontinuous. The Free-Porous Interface boundary condition implements a number of different conditions on such an interior boundary.

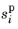
where sri denotes the residual saturation of phase i (which is taken to be equal to zero when the capillary pressure model in the adjacent Phase and Porous Media Transport Properties is user defined), and where denotes the saturation of phase i on the porous side of the interface. This condition is implemented for the Residual saturation option.

In the case that one would like to set a maximum saturation on the porous side of the interface that is larger than the residual saturation, one can use the Outflow, no flux below threshold saturation option. This implements the following Signorini-type condition:

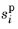
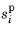
Here s0,i is the threshold saturation below which the saturation should remain, and n·(ρiui) the mass flux out of the porous domain of phase i (it is assumed that the vector n normal to the interface is pointing out of the porous domain). This means that the second inequality implies that phase i is only allowed to flow out of the porous domain. The last equality ensures that when the saturation is below, and not equal to, the threshold value, the flux of phase i across the free-porous interface is zero.

When the droplets, bubbles or particles of a phase i are smaller than the maximum pore size but still larger than the minimum pore size, only a fraction of all pores are accessible for these droplets, bubbles or particles. In that case one can use the Ratio of free flow volume fraction option to apply the following condition on the free-porous interface:

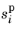
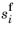
Here r0,i is the ratio between the phase saturation on the porous side and the phase volume fraction on the free-flow side of the free-porous interface.

For all three options, the additional condition is continuity of the fluxes for all phases and it is assumed that the pressure of the phase ic computed from the volume constraint is continuous over the free-porous interface. Note that this last condition assumes that this phase is present on both sides of the interface. In addition, this boundary condition assumes that the phase ic computed from the volume constraint is the wetting phase and it is necessary that the settings for the van Genuchten or Brooks and Corey capillary pressure model in the adjacent porous domains match this assumption.