Here εp (dimensionless) is the porosity, and the vector ui should now be interpreted as the volumetric flux of phase i (SI unit m3/(m2·s) or m/s). The volumetric fluxes are determined using the extended Darcy’s law (Ref. 2)

where κ denotes the permeability (SI unit: m2) of the porous medium, g the gravitational acceleration vector (SI unit m/s2), and μi the dynamic viscosity (SI unit: kg/(m·s)), pi the pressure field (SI unit: Pa), and κri the relative permeability (dimensionless) of phase i, respectively.

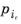
One phase pressure can be chosen independently, which in the Phase Transport in Porous Media interface is chosen to be the phase pressure, , of the phase computed from the volume constraint, and the other phase pressures are defined by the following N − 1 capillary pressure relations:

Substituting Equation 6-100 into Equation 6-99, and using the volume constraint in Equation 6-124, we arrive at the following N − 1 equations for the phase volume fractions si, (i ≠ ic) that are solved in the Phase Transport in Porous Media interface: