The following continuity relations hold for the continuous and dispersed phases (Ref. 3):

Here ϕ (dimensionless) denotes the phase volume fraction, ρ (SI unit: kg/m3) is the density, u (SI unit: m/s) the velocity of each phase, and mdc is the mass transfer rate from the dispersed to the continuous phase (SI unit: kg/(m3·s)). The subscripts c and d denote quantities relating to the continuous and the dispersed and phase, respectively. The following relation between the volume fractions must hold

Both phases are considered to be incompressible, in which case Equation 6-51 and Equation 6-52 can be simplified as:

If Equation 6-54 and Equation 6-53 are added together, a continuity equation for the mixture is obtained:

In order to control the mass balance of the two phases, the Euler–Euler Model interfaces solves Equation 6-54 together with Equation 6-55. Equation 6-54 is used to compute the volume fraction of the dispersed phase, and Equation 6-55 is used to compute the mixture pressure.

The momentum equations for the continuous and dispersed phases, using the nonconservative forms (see for example Ref. 3 or Ref. 9), are:

Here p (SI unit: Pa) is the mixture pressure, which is assumed to be equal for the two phases. In the momentum equations the viscous stress tensor for each phase is denoted by τ (SI unit: Pa), g (SI unit: m/s2) is the vector of gravitational acceleration, Fm (SI unit: N/m3) is the interphase momentum transfer term (that is, the volume force exerted on each phase by the other phase), F (SI unit: N/m3) is any other volume force term, and uint is the interphase velocity (SI unit: m/s).

For fluid-solid mixtures where ρd >> ρc, Equation 6-57 is modified in the manner of Enwald (Ref. 5)

where ps (SI unit: Pa) is the solid pressure.

where 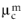and (SI unit: Pa·s) are the dynamic viscosity model of the respective phase. Observe how the viscous terms in equation Equation 6-56 and Equation 6-57 appear with their volume fractions outside the divergence operators. The equations can also be derived so that the terms read ∇ ⋅ (ϕcτc) and ∇ ⋅ (ϕdτd) instead (see for example Ref. 4 or Ref. 5). It depends on exactly how the derivation is carried out. formulation in Equation 6-56 and Equation 6-57 are so that the momentum equation can be divided by ϕc and ϕd respectively as described below.

A simple mixture viscosity covering the entire range of particle concentrations is the Krieger type model (Ref. 5):

Here ϕd,max is the maximum packing limit, by default 0.62 for solid particles. Equation 6-62 can be applied when μc << μd. An extension of Equation 6-62 can be applied for liquid droplets/bubbles:

For liquid droplets/bubbles the default value of ϕd,max is 1.

An alternative to mixture viscosity for dispersed solid particles, that is particles in gas flow, is to model the particle interface with a solid pressure instead (see Solid Pressure). A small viscosity is however necessary for numerical robustness and Gidaspow (Ref. 6) suggested to use

This is consistent with the requirement that 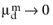when ϕd → 0 (Ref. 9), but in practice it can suffice with any small enough, nonzero value.

In all the equations, Fm denotes the interphase momentum transfer, that is the force imposed on one phase by the other phase. Considering a particle, droplet, or bubble in a fluid flow, it is affected by a number of forces, for example, the drag force, the added mass force, the Basset force, and the lift force. The most important force is usually the drag force, especially in fluids with a high concentration of dispersed solids, and hence this is the predefined force included in the Euler–Euler model. The drag force added to the momentum equation is defined as:

where β is a drag force coefficient and the slip velocity is defined as

The drag force coefficient, β, is for solid particles often written as (Ref. 2)

For fluid-fluid system, Equation 6-67 is regularized to read (Ref. 12)

which is consistent with a vanishing β if ϕc → 0. All drag force models except Gidaspow are based on Equation 6-67 for solid particles and on Equation 6-68 for bubbles and droplets.

For dense particle flows with a high concentration of the dispersed phase — for example, in fluidized bed models — the Gidaspow model (Ref. 6) for the drag coefficient can be used. It combines the Wen and Yu (Ref. 7) fluidized state expression:

For ϕc > 0.8

with the Ergun (Ref. 8) packed bed expression:

For ϕc < 0.8

In the above equations, dd (SI unit: m) is the dispersed particle diameter, and Cd is the drag coefficient for a single dispersed particle. The drag coefficient is in general a function of the particle Reynolds number

No universally valid expression for the drag coefficient exists. Using the implemented Gidaspow model, Cd is computed using the Schiller–Naumann relation.

The Schiller–Naumann model describes the drag coefficient in Equation 6-67 and Equation 6-68 for a single rigid sphere (see for example Ref. 3)

It is valid for particle Reynolds numbers up to some critical Reynolds number, approximately equal to 2.5·105 where drag crisis occurs.

The Schiller–Naumann model is appropriate for diluted flows since the correlation in Equation 6-71 is based on a single particle and does not take particle-particle interaction into account.

The Ishii–Zuber model (Ref. 10) can for solid particles be regarded as a generalization of the Schiller–Naumann model. For solid particles it can be formulated as

and Rem is a Reynolds number based on the mixture viscosity

The Ishii–Zuber model is formulated with the assumption that μm is described by a Krieger type model (Equation 6-62 for solids or Equation 6-63 for droplets and bubbles). The dependence on μm means that the Ishii–Zuber model is valid also for dense suspensions.

where in turn g is the gravitational constant and σ is the surface tension coefficient. The Eötvös number relates surface tension forces to gravitational forces. The second, “distorted” regime ends when hydrodynamic instabilities prevents the drag from increasing further and the distorted regime is capped by the following value:

where A, B, C, and D are empirical correlations of the particle sphericity (see Slip Velocity Models for further details).

Tomiyama and others (Ref. 11) provided three correlations for diluted bubbles and droplets. The correlation for purified fluids read

Fluid pure enough for Equation 6-80 to be valid is typically only achievable in laboratory environments. Even small amounts of surface-active impurities can collect at the droplet/bubble interface and cause a surface tension gradient which resists surface movement. The correlation for slightly contaminated fluids therefore prescribe a slightly higher drag coefficient:

For fluid-solid mixtures where ρd >> ρc, for example solid particles in gas flow, a model for the solid pressure, ps in Equation 6-60, is needed. The solid pressure models the particle interaction due to collisions and friction between the particles. The solid pressure model implemented uses a gradient diffusion based assumption:

where the empirical function G can be thought of as a modulus of elasticity or powder modulus. A common form for G is (Ref. 5)

The available predefined models (all defined in Ref. 5) are those of Gidaspow and Ettehadieh,

in Equation 6-59. Also, ϕd is a degree of freedom and can therefore, during computations, obtain unphysical values in small areas. This can, in turn, lead to unphysical values of material properties such as viscosity and density. To avoid these problems, the implementation uses the following regularizations: