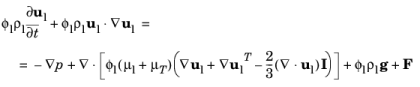The two-fluid Euler–Euler Model is a general, macroscopic model for two-phase fluid flow. It treats the two phases as interpenetrating media, tracking the averaged concentration of the phases. One velocity field is associated with each phase. A momentum balance equation and a continuity equation describe the dynamics of each of the phases. The bubbly flow model is a simplification of the two-fluid model, relying on the following assumptions:

In Equation 6-30, the variables are as follows:

where mgl is the mass transfer rate from the gas to the liquid (SI unit: kg/(m3·s)).

For low gas volume fractions (), you can replace the momentum equations, Equation 6-30, and the continuity equation, Equation 6-31, by

By default, the Laminar Bubbly Flow interface uses Equation 6-33 and 6-34. To switch to Equation 6-30 and 6-31, click to clear the Low gas concentration check box under the Physical Model section.

The physics interface solves for ul, p, and

the effective gas density. The gas velocity ug is the sum of the following velocities:

where uslip is the relative velocity between the phases and udrift is a drift velocity (see Turbulence Modeling in Bubbly Flow Applications). The physics interface calculates the gas density from the ideal gas law:

where M is the molecular weight of the gas (SI unit: kg/mol), R is the ideal gas constant (8.314472 J/(mol·K)), pref a reference pressure (SI unit: Pa), and T is temperature (SI unit: K). pref is a scalar variable, which by default is 1 atm (1 atmosphere or 101,325 Pa). The liquid volume fraction is calculated from

Here, μT is the turbulent viscosity, and σT is the turbulent Schmidt number.

Inserting Equation 6-36 and Equation 6-35 into Equation 6-32 gives

It is possible to account for mass transfer between the two phases by specifying an expression for the mass transfer rate from the gas to the liquid mgl (SI unit: kg/(m3·s)).

The mass transfer rate typically depends on the interfacial area between the two phases. An example is when gas dissolves into a liquid. In order to determine the interfacial area, it is necessary to solve for the bubble number density (that is, the number of bubbles per volume) in addition to the phase volume fraction. The Bubbly Flow interface assumes that the gas bubbles can expand or shrink but not completely vanish, merge, or split. The conservation of the number density n (SI unit: 1/m3) then gives

The number density and the volume fraction of gas give the interfacial area per unit volume (SI unit: m2/m3):

The simplest possible approximation for the slip velocity uslip is to assume that the bubbles always follow the liquid phase; that is, uslip = 0. This is known as homogeneous flow.

A better model can be obtained from the momentum equation for the gas phase. Comparing size of different terms, it can be argued that the equation can be reduced to a balance between the viscous drag force, fD and the pressure gradient (Ref. 3), a so called pressure-drag balance:

Here fD can be written as

where in turn db (SI unit: m) is the bubble diameter, and Cd (dimensionless) is the viscous drag coefficient. Given Cd and db, Equation 6-37 can be used to calculate the slip velocity. In practice, Equation 6-37 is multiplied by ϕl to reduce the slip velocity for large values of ϕg.

Schwarz and Turner (Ref. 4) proposed a linearized version of Equation 6-38 appropriate for air bubbles of 1–10 mm mean diameter in water:

The Hadamard–Rybczynski model is appropriate for small spherical bubbles with diameter less than 2 mm, and bubble Reynolds number less than one. The model uses the following expression for the drag coefficient (Ref. 5):

For bubbles with diameter larger than 2 mm, the model suggested by Sokolichin, Eigenberger, and Lapin (Ref. 1) is a more appropriate choice:

where Eö is the Eötvös number

Here, g is the magnitude of the gravity vector and σ the surface tension coefficient.