Analogous to the single-phase flow wall functions (see Wall Functions applied for the Wall boundary condition), there is a theoretical gap between the solid wall and the computational domain of the fluid. This gap is often ignored when the computational geometry is drawn.

Assuming that the turbulent heat and mass transfer in the near-wall region are analogous, the same type of wall functions used for the temperature (Ref. 8) is also applicable for the mass transport. The mass transfer wall function is formulated as a function of the molecular and turbulent Schmidt numbers of each species, instead of the corresponding Prandtl numbers.

Assume that there is a mass fraction ωi,w just outside the wall and that it is in equilibrium with the surface chemistry. The mass flux, for species i, between the wall and a fluid with a mass fraction of ωi,f at the lift-off position is

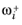
where ρ is the fluid density, Cμ is a turbulence modeling constant, and k is the turbulent kinetic energy. is the dimensionless mass fraction given by (Ref. 8)

κv is the von Kármán constant, and Di,m the mean species diffusion coefficient. The latter corresponds directly to the mixture-averaged diffusion coefficient when using the Mixture-average diffusion model. Using the Fick’s law diffusion model, the mean diffusion coefficient is computed as 1/N·tr(Di), where Di is the diffusion tensor and N is the dimension of the model.

The computational result should be checked so that the distance between the computational fluid domain and the wall, δw, is almost everywhere small compared to any geometrical quantity of interest. The distance δw is available as a postprocessing variable (delta_w) on boundaries.