Nonisothermal Reacting Flow
When a Chemistry interface and a Heat Transfer interface are used in the Nonisothermal Reacting Flow multiphysics coupling, the heat equation is modified to account for reactions and diffusion.
In presence of chemical reactions, the enthalpy (SI unit: J/kg) is a function of temperature, pressure and the mixture composition. For a mixture of N components, the mass fractions verify the condition ω1 + … + ωN = 1. Therefore the enthalpy is a function of the temperature, pressure, and only N − 1 mass fractions:
Assuming the same velocity for the convection term of all components, the mass fractions follow the equation:
On the other hand, using the chain rule, the enthalpy variation is written:
which can be rewritten using the partial molar enthalpies:
Additionally, the heat balance equation in terms of internal energy is written:
where Qvd is the heat source from viscous dissipation, and Q represents additional sources. The heat flux q consists in a term of conduction and a term of diffusion:
Enthalpy and internal energy are linked through the formula , we can thus rewrite the heat balance equation in terms of enthalpy:
Introducing the heat capacity at constant pressure Cp (SI unit: J/(kg·m3), and the coefficient of thermal expansion αp (SI unit: 1/K) gives:
The term with the pressure derivative is the work of pressure forces Qp. The enthalpy variation due to the gradient of species mass flux can be partly simplified with the diffusion part of the heat flux. The heat source of reaction can be written in terms of enthalpies of reaction Hi instead of partial enthalpies (see Ref. 9). The temperature derivative term can be expanded to make the convective term appear. We finally obtain the temperature equation for a free flow with N species and M reactions:
For reacting flows moving through the interstices of a porous medium, the heat sources of reaction and diffusion are only accounted for the temperature of the fluid phase. While the porosity is already accounted for in the diffusion term through the mass flux, the heat source of reaction has to be multiplied by the porosity. Also, in presence of a porous catalyst, both reactions in the bulk and reactions at the surface are accounted for in the reaction source term:
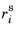
where εp is the porosity of the medium (SI unit: 1), Sarea is the specific surface area (SI unit: 1/m), and is the surface reaction rate (SI unit: mol/(m2·s)).
An additional source term is added to model convective heat transfer between the fluid and the porous matrix to get the temperature equation for nonisothermal reacting flows in porous media:
This equation is the one that is solved when the Porous medium type of the Porous Medium feature is set to Local thermal nonequilibrium, since both fluid and porous matrix temperatures are solved separately. With the Local thermal equilibrium approach, the equation is written for the common temperature, and in terms of effective material properties for the time derivative term and conduction term: